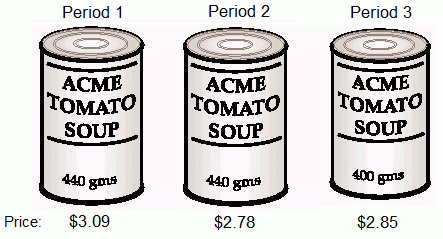CPI movements over the past 70 years
[["Dec 1945","Mar 1946","Jun 1946","Sep 1946","Dec 1946","Mar 1947","Jun 1947","Sep 1947","Dec 1947","Mar 1948","Jun 1948","Sep 1948","Dec 1948","Mar 1949","Jun 1949","Sep 1949","Dec 1949","Mar 1950","Jun 1950","Sep 1950","Dec 1950","Mar 1951","Jun 1951","Sep 1951","Dec 1951","Mar 1952","Jun 1952","Sep 1952","Dec 1952","Mar 1953","Jun 1953","Sep 1953","Dec 1953","Mar 1954","Jun 1954","Sep 1954","Dec 1954","Mar 1955","Jun 1955","Sep 1955","Dec 1955","Mar 1956","Jun 1956","Sep 1956","Dec 1956","Mar 1957","Jun 1957","Sep 1957","Dec 1957","Mar 1958","Jun 1958","Sep 1958","Dec 1958","Mar 1959","Jun 1959","Sep 1959","Dec 1959","Mar 1960","Jun 1960","Sep 1960","Dec 1960","Mar 1961","Jun 1961","Sep 1961","Dec 1961","Mar 1962","Jun 1962","Sep 1962","Dec 1962","Mar 1963","Jun 1963","Sep 1963","Dec 1963","Mar 1964","Jun 1964","Sep 1964","Dec 1964","Mar 1965","Jun 1965","Sep 1965","Dec 1965","Mar 1966","Jun 1966","Sep 1966","Dec 1966","Mar 1967","Jun 1967","Sep 1967","Dec 1967","Mar 1968","Jun 1968","Sep 1968","Dec 1968","Mar 1969","Jun 1969","Sep 1969","Dec 1969","Mar 1970","Jun 1970","Sep 1970","Dec 1970","Mar 1971","Jun 1971","Sep 1971","Dec 1971","Mar 1972","Jun 1972","Sep 1972","Dec 1972","Mar 1973","Jun 1973","Sep 1973","Dec 1973","Mar 1974","Jun 1974","Sep 1974","Dec 1974","Mar 1975","Jun 1975","Sep 1975","Dec 1975","Mar 1976","Jun 1976","Sep 1976","Dec 1976","Mar 1977","Jun 1977","Sep 1977","Dec 1977","Mar 1978","Jun 1978","Sep 1978","Dec 1978","Mar 1979","Jun 1979","Sep 1979","Dec 1979","Mar 1980","Jun 1980","Sep 1980","Dec 1980","Mar 1981","Jun 1981","Sep 1981","Dec 1981","Mar 1982","Jun 1982","Sep 1982","Dec 1982","Mar 1983","Jun 1983","Sep 1983","Dec 1983","Mar 1984","Jun 1984","Sep 1984","Dec 1984","Mar 1985","Jun 1985","Sep 1985","Dec 1985","Mar 1986","Jun 1986","Sep 1986","Dec 1986","Mar 1987","Jun 1987","Sep 1987","Dec 1987","Mar 1988","Jun 1988","Sep 1988","Dec 1988","Mar 1989","Jun 1989","Sep 1989","Dec 1989","Mar 1990","Jun 1990","Sep 1990","Dec 1990","Mar 1991","Jun 1991","Sep 1991","Dec 1991","Mar 1992","Jun 1992","Sep 1992","Dec 1992","Mar 1993","Jun 1993","Sep 1993","Dec 1993","Mar 1994","Jun 1994","Sep 1994","Dec 1994","Mar 1995","Jun 1995","Sep 1995","Dec 1995","Mar 1996","Jun 1996","Sep 1996","Dec 1996","Mar 1997","Jun 1997","Sep 1997","Dec 1997","Mar 1998","Jun 1998","Sep 1998","Dec 1998","Mar 1999","Jun 1999","Sep 1999","Dec 1999","Mar 2000","Jun 2000","Sep 2000","Dec 2000","Mar 2001","Jun 2001","Sep 2001","Dec 2001","Mar 2002","Jun 2002","Sep 2002","Dec 2002","Mar 2003","Jun 2003","Sep 2003","Dec 2003","Mar 2004","Jun 2004","Sep 2004","Dec 2004","Mar 2005","Jun 2005","Sep 2005","Dec 2005","Mar 2006","Jun 2006","Sep 2006","Dec 2006","Mar 2007","Jun 2007","Sep 2007","Dec 2007","Mar 2008","Jun 2008","Sep 2008","Dec 2008","Mar 2009","Jun 2009","Sep 2009","Dec 2009","Mar 2010","Jun 2010","Sep 2010","Dec 2010","Mar 2011","Jun 2011","Sep 2011","Dec 2011","Mar 2012","Jun 2012","Sep 2012","Dec 2012","Mar 2013","Jun 2013","Sep 2013","Dec 2013","Mar 2014","Jun 2014","Sep 2014","Dec 2014","Mar 2015","Jun 2015","Sep 2015","Dec 2015","Mar 2016","Jun 2016","Sep 2016","Dec 2016","Mar 2017","Jun 2017","Sep 2017"],[[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[10.800000000000001],[7.9000000000000004],[7.7000000000000002],[7.5],[7.2999999999999998],[12.199999999999999],[14.300000000000001],[18.600000000000001],[20.5],[23.899999999999999],[22.899999999999999],[19.600000000000001],[17],[10.5],[6.7999999999999998],[4.9000000000000004],[4.7999999999999998],[1.6000000000000001],[3.2000000000000002],[1.6000000000000001],[0],[1.6000000000000001],[0],[1.5],[1.5],[3.1000000000000001],[3.1000000000000001],[6.0999999999999996],[7.5999999999999996],[6],[6],[2.8999999999999999],[1.3999999999999999],[1.3999999999999999],[1.3999999999999999],[0],[0],[1.3999999999999999],[1.3999999999999999],[1.3999999999999999],[2.7999999999999998],[2.7000000000000002],[2.7000000000000002],[4.0999999999999996],[4.0999999999999996],[4],[4],[3.8999999999999999],[1.3],[0],[0],[-1.3],[0],[0],[0],[0],[1.3],[1.3],[2.6000000000000001],[2.6000000000000001],[2.5],[3.7999999999999998],[2.5],[3.7999999999999998],[3.7000000000000002],[3.7000000000000002],[4.9000000000000004],[3.6000000000000001],[2.3999999999999999],[2.3999999999999999],[2.2999999999999998],[3.5],[4.7000000000000002],[3.3999999999999999],[3.3999999999999999],[2.2000000000000002],[2.2000000000000002],[2.2000000000000002],[3.2999999999999998],[3.2999999999999998],[3.2999999999999998],[3.2999999999999998],[2.1000000000000001],[3.2000000000000002],[3.2000000000000002],[5.2999999999999998],[5.2000000000000002],[5.2000000000000002],[7.0999999999999996],[7],[6.9000000000000004],[6.9000000000000004],[5.7000000000000002],[4.7000000000000002],[5.5999999999999996],[8.3000000000000007],[9.9000000000000004],[12.5],[14],[14.4],[16.399999999999999],[16.699999999999999],[17.699999999999999],[17],[12],[14.300000000000001],[13.1],[12],[13.800000000000001],[14.300000000000001],[13.300000000000001],[13.6],[13.300000000000001],[9.4000000000000004],[8.6999999999999993],[8],[7.7999999999999998],[7.5999999999999996],[8],[8.8000000000000007],[9.5],[10.199999999999999],[10.4],[11],[9.9000000000000004],[9.1999999999999993],[9.4000000000000004],[8.4000000000000004],[9],[11],[10.800000000000001],[10.9],[12.4],[11.300000000000001],[11.4],[11.1],[9.1999999999999993],[8.5999999999999996],[5.7999999999999998],[4],[3.7000000000000002],[2.5],[4.4000000000000004],[6.5999999999999996],[7.5999999999999996],[8.3000000000000007],[9.1999999999999993],[8.5],[8.8000000000000007],[9.5999999999999996],[9.4000000000000004],[9.3000000000000007],[8.3000000000000007],[7.2000000000000002],[6.7999999999999998],[7.2000000000000002],[7.2999999999999998],[7.5999999999999996],[6.7999999999999998],[7.5],[8],[7.7999999999999998],[8.6999999999999993],[7.7000000000000002],[6.0999999999999996],[6.9000000000000004],[4.7999999999999998],[3.2999999999999998],[3.1000000000000001],[1.5],[1.7],[1.2],[0.80000000000000004],[0.29999999999999999],[1.2],[1.8],[2.2000000000000002],[1.8],[1.5],[1.8],[2],[2.6000000000000001],[3.7000000000000002],[4.5],[5.0999999999999996],[5.0999999999999996],[3.7999999999999998],[3.1000000000000001],[2.1000000000000001],[1.5],[1.3999999999999999],[0.29999999999999999],[-0.40000000000000002],[-0.29999999999999999],[-0.10000000000000001],[0.69999999999999996],[1.3999999999999999],[1.5],[1.2],[1],[1.8],[1.8999999999999999],[2.7999999999999998],[3.1000000000000001],[6.0999999999999996],[5.7999999999999998],[6],[6.0999999999999996],[2.5],[3.1000000000000001],[3],[2.7999999999999998],[3.2000000000000002],[2.8999999999999999],[3.2999999999999998],[2.6000000000000001],[2.6000000000000001],[2.3999999999999999],[2],[2.5],[2.2999999999999998],[2.5],[2.3999999999999999],[2.5],[3.1000000000000001],[2.7999999999999998],[2.8999999999999999],[4],[4],[3.2999999999999998],[2.5],[2.1000000000000001],[1.8],[2.8999999999999999],[4.2999999999999998],[4.4000000000000004],[5],[3.7000000000000002],[2.3999999999999999],[1.3999999999999999],[1.2],[2.1000000000000001],[2.8999999999999999],[3.1000000000000001],[2.8999999999999999],[2.7999999999999998],[3.2999999999999998],[3.5],[3.3999999999999999],[3],[1.6000000000000001],[1.2],[2],[2.2000000000000002],[2.5],[2.3999999999999999],[2.2000000000000002],[2.7000000000000002],[2.8999999999999999],[3],[2.2999999999999998],[1.7],[1.3],[1.5],[1.5],[1.7],[1.3],[1],[1.3],[1.5],[2.1000000000000001],[1.8999999999999999],[1.8]]]
[]
[{"axis_id":"0","tick_interval":"6","axis_min":"","axis_max":"","axis_title":"","precision":-1,"axis_units":"","tooltip_units":"","table_units":"","data_unit_prefix":"","data_unit_suffix":"","reverse_axis":false}][{"axis_id":"0","tick_interval":"","axis_min":"-10","axis_max":"","axis_title":"% change (a)","precision":"","table_units":"(%)","tooltip_units":"(%)","axis_units":"","data_unit_prefix":"","data_unit_suffix":"","reverse_axis":false}]