Jason Annabel, Qinghuan Luo (ABS) and Aaron Nicholas (Deakin University)¹
University output measures in the Australian National Accounts: experimental estimates, 2008 to 2017
This paper describes new experimental indexes for the volume of Australian university output
Introduction
The output of public universities is substantial. In 2016/17, services provided by technical, vocational and tertiary education institutions contributed 40% of education industry output.² In the same year, higher education accounted for 25% of Australia’s exports of services.³
The ABS currently estimates the annual change in the volume of universities output using the change in student enrolments, measured on a full-time equivalent basis.
The experimental output index derived in this paper grows at a similar rate to the current ABS index. However, the proposed index has two main advantages. It uses:
- a direct measure of research output; and
- applies expenditure weights to enrolment data to implicitly capture some aspects of quality change.
In addition, teaching services provided by universities have continued to evolve, and this evolution is continuing as a result of COVID-19. The output measures proposed in this paper provide greater scope for incorporating future compositional and quality change.
There is little consistent disaggregated data relating to the volume of university output, which is a barrier to measurement. The experimental indexes in this paper are based on datasets published by the Commonwealth Department of Education, Skills and Employment, covering all 37 public universities. The ABS worked closely with Dr Aaron Nicholas of Deakin University on the analysis presented here.
The ABS invites feedback from the public on the experimental methods proposed in this paper. For further discussion of these methods please contact the ABS at economic.research@abs.gov.au.
Footnotes
- The authors would like to acknowledge the assistance of Amani Elnasri and Kristen Stone in preparing this paper.
- See https://www.abs.gov.au/AUSSTATS/abs@.nsf/Lookup/5217.0Main+Features12017-18 Estimates from the 2016-17 input-output tables show that tertiary higher education services contributes approximately 27% of total supply of the entire education industry, see https://www.abs.gov.au/AUSSTATS/abs@.nsf/DetailsPage/5215.0.55.0012016-17?OpenDocument
- https://www.abs.gov.au/AUSSTATS/abs@.nsf/Lookup/5368.0.55.003Main+Features12018-19?OpenDocument
Classification of public universities
Non-market output occurs when goods and services are provided free of charge, or at prices which are not economically significant. These are prices that have no significant effect on the amount that producers are willing to supply and the amounts purchasers wish to buy.⁴
The ABS examines each producing unit in the economy to determine whether it charges economically significant prices for its output. Units that predominantly charge prices that are not economically significant are classified as non-market producers.
Public universities are classified as non-market producers as they deliver services to domestic undergraduate students at prices which are not deemed to be economically significant and they engage in significant amounts of non-market public research activities.
As universities are entities under the control of State and Commonwealth governments, they are classified to the general government sector in macroeconomic statistics. More information on the institutional sector classification used in Australia can be found in Standard Economic Sector Classifications of Australia (ABS Cat. no. 1218.0).⁵
Private universities are considered to produce market output and are outside the scope of this paper, although improvements to measurement of this small sub-sector may also be considered in future work.
The indexes proposed in this paper relate to the public sector component of the Australian and New Zealand Standard Industrial Classification (ANZSIC) class 8102 – Higher Education.
Public schools (within ANZSIC group 802) and some vocational education and training institutions (ANZSIC class 8101) are also non-market producers. Therefore, the Education and Training industry (ANZSIC Division P) contains significant amounts of non-market output (in contrast to most industries in Australia, which contain only a small proportion of non-market production). This makes it hard to measure the productivity of this industry. As a result, the ABS currently excludes the Education and Training industry from published multifactor productivity statistics.
For further information about the conceptual framework which underpins the measurement of non-market output, please refer to "Non-market output measures in the Australian National Accounts: a conceptual framework for enhancements".⁶
Overview of methodology
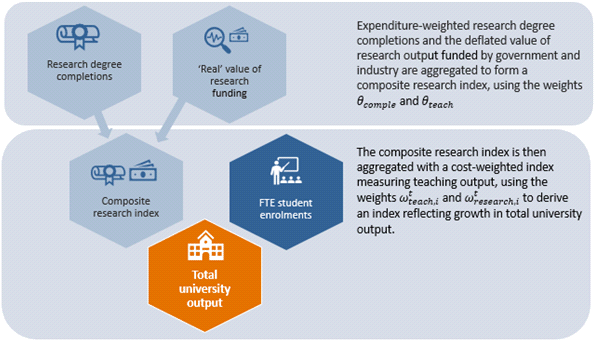
The output of public universities is comprised of two broad streams: (a) teaching output; and (b) research output. Research output can be sub-divided into: (i) research degree completions; and (ii) research funded by government and industry. The existing ABS measure of the output of public universities is based on student enrolment numbers, and is therefore a measure of teaching output alone. The experimental estimates proposed in this paper integrate all three streams of output (one teaching and two research) and incorporate a quality dimension via the application of expenditure weights.
Changes in the volume of output for each of these streams of activity can be measured by compiling a volume index. A volume index for a particular product reflects the change in how much more or less of that product has been produced from one period to the next, with the impact of price changes removed. A volume index that represents an aggregate of all products produced (e.g. total output for an economy) requires a method to weight the products together.
In the case of public universities, the operating costs incurred by each university are used as weights. This type of expenditure data is used to weight the outputs instead of prices, which are not meaningful in the context of non-market production because prices are not deemed to be economically significant.
The intuition underlying this is that cost differences across the sector implicitly convey information about the relative quality of universities. A university that incurs greater costs in producing its output (perhaps by paying higher salaries to attract the best academic staff, or by enrolling fewer students per lecturer) is assumed to offer a higher quality service, and therefore its activity carries a higher weight in aggregation. In other words, universities that spend more on each unit of teaching and/or research effectively produce higher quality outputs. This intuition is discussed in depth in Schreyer (2010) and Diewert (2008, 2010).
Teaching output measures
The quantity of teaching output delivered by universities was measured in terms of enrolled student load, on a full-time equivalent basis. Enrolment information was sourced from the Department of Education.⁷ Non-award qualifications were excluded, as were research-based degrees (the latter contributed to a subsequent stream of output). A volume index was constructed by weighting the student enrolment data for each university with the corresponding expenditure data allocated to teaching activities, and aggregating across universities.
This experimental method has some limitations, including:
- Using student enrolments as the quantity measure instead of student completions means that degrees that take longer to complete (e.g. medicine and law) carry a higher weight. But this also applies to students who take longer to complete their degrees (e.g. due to subject failures etc). A student who repeats a unit will be allocated a higher weight because they remain enrolled for longer than their counterparts who complete the degree without failure. This is because an academic who delivers a course to a student for a second time is producing additional output.
- Ideally, a higher weight would be assigned to degrees that are more expensive to deliver. For instance, a chemistry degree is likely to be more costly for a university to deliver (and therefore more ‘valuable’ to a student) than a humanities degree. Enrolments data by discipline are publicly available, but this cannot be used in the construction of a volume index because expenditures incurred per faculty are not available.
- No explicit differentiation is possible between different levels of qualifications (e.g. one year spent on a coursework masters degree versus a year spent on an undergraduate degree).
Research output measures
While research is a core function of universities, there is no clear definition of research output, which makes it hard to measure. In addition, there have been several changes to the method used to allocate government funding for research in recent years.
For output measurement purposes, two experimental research output indexes have been calculated. The data used in these indexes has been sourced from the Department of Education.⁸
Research degree completions
The first index reflects the number of research degree completions per university. Research degrees are either research doctorate (PhD) or research-based masters degree qualifications. Doctoral degrees were treated as being equivalent to two research masters completions. These were aggregated across all universities using the research expenditure weights for each university in each year, a process which is described in more detail later in the paper.
Research output funded by government and industry
The second index represents university research output funded by government and industry. Since in many cases university research output cannot be observed and quantified, this measure is proxied by the amount of research income received by universities from both public and industry bodies in the form of grants. The assumption is that this income is typically tied to the production of knowledge in the form of reports and publications. Research grant income data was sourced from the Department of Education, and a ‘real’ measure of research income was obtained by deflating these values by the Consumer Price Index. These were also aggregated across all universities using the research expenditure weights for each university in each year, as described later in the paper.
Ideally, a metric of the tangible research output of universities, such as counts of research publications, would be used to supplement this index. However, publication counts suffer from a lack of quality adjustment. It might be possible to incorporate a quality perspective by weighting each publication by the number of citations, but this would be very resource-intensive.
Combining the two research indexes
The two research indexes described above need to be combined to produce a composite index that reflects both the number of research degree completions and the amount of research funded by government and industry. Government funding policies have varied over time, which makes it difficult to find a consistent way to aggregate these two indexes. To allow future periods to be easily incorporated into the index, the government’s most recent funding rule, of 2017, was chosen to derive aggregation weights.⁹
In 2017, two government university research support programs were established: the Research Support Program (RSP); and the Research Training Program (RTP). The RSP funds the systemic cost of university research not already supported through specific research projects, such as libraries, laboratories, consumables, and computing centres whereas the RTP funds scholarships to support the training of students undertaking higher degrees by research.
The government allocates RSP funding purely on the basis of performance in research grant income generation (including both government and industry grants). 50% of RTP is allocated on the basis of research grant income generation and 50% on the basis of research degree completions. Using 2017 data, total RSP funding to universities was added to half of the total RTP funding, and this figure was divided by the combined total of RSP and RTP funding to derive the proportion of funding based on research grant success. The proportion is estimated to be about 73%, which was used as the relative weight for research output funded by government and industry. The residual 27% was used as the relative weight for research degree completions. (This calculation is outlined in greater detail in the technical appendix.) These weights are used to combine the two research activities into a composite index of research output.
Obtaining cost weights for research and teaching
Total expenditure data for each university is publicly available from the Department of Education website.¹⁰ To calculate expenditure-weighted indexes for teaching output and research output, costs need to be split accordingly. However, neither the Department of Education nor the universities themselves disaggregate these expenditures between teaching and research. In fact, these activities may overlap so closely (most academics are expected to do both) that it might not be meaningful for a university to perform such a disaggregation.
In this analysis, each university’s total operating expenditure was split into teaching and research components. There are three categories of academic staff: teaching only staff, research only staff, and staff with a combined role in teaching and research.¹¹ As there is no data available to split the third category into underlying teaching and research components, we assume the shares of time spent on research and teaching by academic staff from the combined category are 25% and 75%. This is an arbitrary split, designed to provide a conservative estimate of research activity for the combined academic staff group in the absence of further information. These shares are used to weight the research and teaching output for each university. Gathering data on the actual split would be a key enhancement to the experimental index. Sensitivity analysis demonstrating the impact of this assumption is discussed later in the paper.
The average research weights for individual universities obtained via this process ranged from 0.25 to 0.68, with the highest weights for research activity for universities in the Group of Eight.¹² The proportions of teaching and research also varied across time, with more volatility across smaller universities which have lower student enrolments and smaller research output.
There are a number of drawbacks with this approach, including:
- there is no information on how academics engaged for both teaching and research split their time between these activities. Assuming 25% of this combined category is research may be an underestimate or an overestimate;
- using full time equivalent ratios to split expenditure implicitly assumes the same unit labour cost for research and teaching. Ideally, variation in staff levels should be taken into consideration in splitting expenditure between these activities. Academic staff may vary from research assistants to full-time professors. Staff with such widely differing levels of experience would be expected to receive substantially different pay rates, reflecting differences in the amount and quality of their output. Unfortunately, no adjustment can presently be made to account for these differences; and
- total operating expenditure for each university was split solely on the basis of labour inputs (i.e. academics) – in other words, the contributions of intermediate and capital inputs towards teaching and research activities were not separately determined.
Notwithstanding these caveats, the cost weights derived above were used to aggregate the teaching output and research output indexes, to construct a volume index for the output of the entire public university sector.
Figure 1 provides an overview of the methods used to derive the aggregate experimental university output index.
Figure 1: Compilation of the experimental university output index
Image
Description
Footnotes
- https://www.dese.gov.au/higher-education-publications/finance-publication
- https://www.dese.gov.au/higher-education-statistics/resources/2017-staff-full-time-equivalence
- The ‘Group of Eight’ universities are the University of Western Australia, Monash University, the Australian National University, the University of Adelaide, the University of Melbourne, the University of New South Wales, the University of Queensland and the University of Sydney. https://go8.edu.au/
Results
Figure 2 shows the two components of research activity on an expenditure-weighted basis from 2008 to 2017. As universities report their enrolments and finances on a calendar year basis, all time series shown in this paper were compiled on a calendar year basis.¹³ The time series are volume indexes, with the base year set at 2008. Research degree completions have grown significantly faster than research output funded by government and industry, although, as mentioned earlier, the latter component is the major driver of the composite research index (also shown in Figure 2). The strong growth in research completions largely reflects faster growth in higher research degree enrolments of international students. Enrolments of international students for higher research degrees grew 94.3% from 2008 to 2017 compared to 11.9% for domestic students.¹⁴ Aggregate research output produced by the university sector (as estimated by the composite index) grew by 40.4% over the timespan.
Figure 2 also shows an index of expenditure on research and development by higher educational institutions based on data from the ABS Survey of Research and Experimental Development, Higher Education Organisations for 2018.¹⁵ This series is also expressed in chain volume terms in Figure 2 and grew by 32% over the timespan. The growth in research expenditure tracks closely with the new aggregate experimental estimates of research output which provides a level of validation to the experimental methodology.
Figure 3 shows the composite research index alongside the expenditure-weighted teaching activity index. The two indexes track fairly closely over time. The composite research index grows by 40.4% over the time span compared to 38.5% in the teaching output index.
Figure 4 shows the aggregate university teaching output index based on the experimental methodology in this paper, compared to the current ABS method.¹⁶ The experimental methodology in this paper estimates that university output grew by a cumulative 39.5% over this time period, 2.7 percentage points higher than cumulative growth using the current ABS methodology.
The graph shows that the weighted aggregation of the experimental teaching and research indexes has little statistical impact compared to the current method. While the method proposed in this paper implies slightly stronger output growth over the time span than the current method, the overall economic story is broadly similar.
Growth in university output from 2008 to 2017 is predominantly driven by universities outside the Group of Eight. As shown in Figure 5, these universities collectively grew by a cumulative 49.7%, compared to Group of Eight universities which grew 27.7%.
Footnotes
- Before inclusion in ABS macroeconomic statistics, the estimates in this paper would need to be converted to a financial year basis.
- Table 4, Higher education facts and figures 2019. https://www.universitiesaustralia.edu.au/wp-content/uploads/2019/08/190716-Facts-and-Figures-2019-Final-v2.pdf
- Data from this survey is published in Research and Experimental Development, Higher Education Organisations, Australia, see https://www.abs.gov.au/AUSSTATS/abs@.nsf/Lookup/8111.0Explanatory%20Notes12018?OpenDocument
- The 'current ABS method' in Figure 3 represents a chain volume derivation of output of public universities, sourced from annual supply-use tables and is previously unpublished.
Sensitivity of teaching/research aggregation weights
As indicated earlier, there is currently no way to meaningfully split those academics engaged to perform 'combined' teaching and research services into separate underlying teaching and research components. This paper assumes that these academics spend, on average, 75% of their time on teaching, with the remaining 25% allocated to research.
Two additional models have been estimated. Model 1 shows the result of assuming these academics allocate 50% of their time to teaching with the remaining 50% allocated to research. Model 2 shows the result of assuming these academics spend 100% of their time on teaching. Both models are compared to the 'baseline' method outlined earlier and are illustrated in Figure 6.
Allocating 50% 'combined' academics' time to teaching adds 2.4 percentage points to cumulative university output growth over the time period, while allocating 100% to teaching subtracts 2.4 percentage points from growth over the period.
Next steps - where to from here?
The experimental output index derived in this paper grows at a similar rate to the current ABS index. However, the proposed index has two main advantages. It uses:
- a direct measure of research output; and
- applies expenditure weights to enrolment data to implicitly capture some aspects of quality change between universities.
In addition, teaching provided by universities has continued to evolve, and this evolution is continuing as a result of COVID-19. The output streams proposed in this paper provide greater scope for incorporating future compositional and quality change.
Following a peer review process, and resulting revisions to this work, the ABS will consider incorporating measures based on the experimental index into the Australian National Accounts. There are also a number of possible extensions to this work, which we now turn to.
Refinements to the relative weights of teaching versus research
Information about how academics engaged to undertake both teaching and research activities split their time would provide a basis for calculation of the research and teaching weights. In the absence of a detailed collection to obtain such information, consultation with a number of universities could be undertaken. Additionally, incorporation of data regarding the academic level of staff members of different designations would improve the teaching and research weights, but this data is not available.
The relative weights could also be improved by incorporating intermediate and capital inputs. The method for determining the division of expenditure into teaching and research components using the staff research/teaching designation is simplistic, and assumes that all non-academic operating costs are split according to academic designation. Separate models could be developed to identify the research components of intermediate and capital inputs.
Stratifying teaching output data by discipline
Consideration was given to stratifying teaching activity by discipline, because educating a medical student is likely to be more expensive than educating a humanities student, and therefore should carry greater weight. While the Department of Education publishes enrolments statistics by 'broad field of education', operating costs by discipline do not exist in published form. Individual universities would be likely to collect expenditure by faculty in their management accounts, and this could be an avenue for future inquiry.¹⁷ The Department of Education has recently commissioned a project on estimating expenditure differences across various disciplines, which could prove to be useful.¹⁸
Use of price information
Despite being classified as non-market activity, the public university sector in Australia engages in significant amounts of market-based activity, particularly educating international students. Since these students pay different fees across different universities and courses, this variation could serve as a means by which teaching output could be quality-adjusted. At the current time, this data is not centrally collected. An alternative approach could be to use differences in academic staff salaries across universities, which would reflect differences in the ability of universities to attract higher quality academics, which in turn is an indicator of quality. This approach would have applications in measuring research output as well as teaching. However, once again, such data is not centrally collected or available at this time.
Incorporating research publications within research output measures
Research output is measured using deflated data on research grant funding and higher degree completions. Ideally, research publications should be included in the measure of university research output. One possibility would be to use data from the Australian Research Council (ARC) collected through the Excellence for Research in Australia program (ERA); however, data is not reported on an individual university basis. Efforts to coordinate, extract and compile information from the ARC would help improve the estimates, though the ERA program is only conducted every three years.
Incorporating university ranking data
Some thought has been given to the possibility of weighting each university according to its 'ranking', so that more highly ranked universities carry greater weight.¹⁹ While rankings contain information about which universities are 'perceived to be better', they don’t indicate by how much, which poses difficulties for the construction of weights. This could be an avenue for future research.
Quality adjustment by degree types
While this study has focused on quality differences across universities, it captures them implicitly through cost weights. An alternative quality-adjustment, which is prominent in academic literature, involves explicit outcome-based quality adjustment through differences in the rate of return to education across different qualifications. An example is Gu and Wong (2015). This approach accounts for the fact that a medical degree is likely to reward the student with a higher lifetime salary than some other types of qualification, and therefore should carry greater weight. Such explicit quality adjustments would require additional work to establish the strength of the link between the outcome (lifetime salary) and the output (completion of a degree). It is worth noting that while explicit quality adjustment of non-market economic activity in this manner is an engaging research topic, the ABS is not aware of any country that has implemented such an approach in their national accounts.
Incorporation of private universities
This analysis is restricted to the 37 public universities operating in Australia, but could be extended to include universities and other higher educational institutions owned and controlled by the private sector. This will be considered prior to implementation in the national accounts.
Producing experimental multi-factor productivity statistics
Volume measures of inputs used in the production of outputs, such as labour, capital and intermediate goods and services, would facilitate the derivation of experimental measures of multi-factor productivity for public universities. The ABS will investigate the feasibility of this during 2020/21.
References
Show all
Annabel J (2019), “Enhancing measures of non-market output in economic statistics: Progress paper”, Australian Bureau of Statistics.
Annabel J (2020), “Non-market output measures in the Australian National Accounts: a conceptual framework for enhancements”, Australian Bureau of Statistics.
Diewert W E (2008), “The Measurement of Non-market Sector Outputs and Inputs Using Cost Weights”, University of British Columbia.
Diewert W E (2010), “Measuring Productivity in the Public Sector: Some Conceptual Problems”, University of British Columbia.
Gu W and Wong A (2015), “Productivity and economic output of the education sector”, Journal of Productivity Analysis, 43(2), 165-182.
Norton A and Cherastidtham I (2018), “Mapping Australian higher education 2018, Grattan Institute report”.
Schreyer P (2010), “Towards Measuring the Volume Output of Education and Health Services: A Handbook”, OECD.
Schreyer P (2012), “Output, outcome and quality adjustment in measuring health and education services”. Review of Income and Wealth, 58(2), 257-278.
Technical appendix
Show all
The formulae underlying construction of the composite university output index are outlined below.
Output of a university is composed of teaching output and research output. In the indexes proposed in this paper, research output is proxied by research degree completions and research activity funded by government and industry through research grants, where research grants (deflated by the Consumer Price Index) act as a proxy for the real amount of research funding. So, at the lowest level of disaggregation, university output can be thought to comprise three components: teaching, research degree completions, and research grants.
Year-to-year Laspeyres quantity index
A Laspeyres quantity index from year \(t-1\) to \(t\) for university output activity component \(a\) can be calculated as
\(Q_a^{t-1,t}= \sum\limits_i W^{t-1}_{a,i} \frac{q^t_{a,1}}{q^{t-1}_{a,i}} \) , (1)
where
\(q^t_{a,i}\) is the output quantity indicator for activity component \(a\)
\(a = teach\) (teaching), \(grant\) (research grants) or \(comple\) (research degree completions).
\(W^{t}_{a,i}\) is the individual University \(i\)'s weight for activity \(a\) with \(\sum_{i}W_{a,i}^t=1\) and
the aggregation in (1) is across all universities in the university sector.
The following output quantity indicators are used:
Teaching: Full time student load;
Grants: CPI deflated research grant income; and
Completions: The number of research degree completions, where PhDs are counted as equivalent to two research master degrees.
Derivation of university weights
The weights in (1) are based on the university’s operating expenditure. For each university \(i\) the total expenditure \(e^t_i\) is split into three components: teaching \(\omega^t_{teach,i}e^t_{i}\) grants \(\omega^t_{grant,i}e^t_{i}\) and completions \(\omega^t_{comple,i}e^t_{i}\) where the splits \(\omega^t_{teach,i}\) , \(\omega^t_{grant,i}\) and \(\omega^t_{comple,i}\) can be considered as relative cost proportions within a University with
\(\omega^t_{teach,i}+\omega^t_{grants,i}+\omega^t_{comple,i}=1\) . (2)
The weights \(W^t_{a,i}\) in Eq (1) can be written in the following form for activity \(a\) at the \(i^{th}\) University, at time \(t\).
\(W^t_{a,i} =\frac{\omega^t_{a,i}e^t_i}{\sum_j\omega^t_{a,j}e^t_j}\) . (3)
The weights can be derived in two steps.
First, the university’s total expenditure is split using proportions of teaching \(\omega^t_{teach,i}\) and research \(\omega^t_{res,i}\equiv \omega^t_{grant,i}+\omega^t_{comple,i}\) where \(\omega^t_{teach,i}+\omega^t_{res,i}=1\). The proportion of expenditure on research is estimated using the ratio of academic staff full time equivalent (FTE) in research to total academic staff FTE \((ALL^t_i)\). Assume that research only staff \((RES^t_i)\) have 100% FTE in research. For academics with a combined role in teaching and research \((COMBINED^t_i)\), assume that fraction of their FTE in research is \(x\). Total academic staff FTE in research is\(RES^t_i + x*COMBINED^t_i\) The split between research and teaching can be written as
\(\omega^t_{res,i}=\frac{RES^t_i+x*COMBINED^t_i}{ALL^t_i}, \omega^t_{teach,i}=1-\omega^t_{res,i}\) . (4)
In this analysis, \(x=0.25\)
Second, research expenditure is further split into grants and completions using proportions derived as follows:
\(\omega^t_{grant,i}=\theta_{grant}\omega^t_{res,i}, \omega^t_{comple}=\theta_{comple}\omega^t_{res,i},\theta_{grant}+\theta_{comple}=1\) (5)
where \(\theta_{grant}\) and \(\theta_{comple}\) are the relative proportions of funding based on research grant success and completions of research degrees within in a university.
In this paper \(\theta_{grant}\) and \(\theta_{comple}\) are assumed to be constant across the university sector and estimates of these proportions are based on how Australian government allocates block funding to universities for research. There are currently two government funds: the Research Support Program (RSP) and the Research Training Program (RTP).
The proportion \(\theta_{grant}\) is estimated as follows. In the recent funding rule, 100% of the RSP is allocated based on universities’ performance in attracting research grant income, while only 50% of the RTP is allocated based on research grant income, with the other 50% based on research degree completions. Using the 2017 funding, \(RSP_{2017}=$879 million\) and \(RTP_{2017}=$1,012 million\) thus \(\theta_{grant} \) and \(\theta_{comple}\) are estimated to be
\(\theta_{grant}=\frac{RSP_{2017}+0.5*RTP_{2017}}{RSP_{2017}+RTP_{2017}}\approx 0.73, \theta_{comple}=1-\theta_{grant}\approx0.27\) . (6)
Calculation of quantity indexes for various components and aggregates
(i) Teaching index
The teaching index is calculated directly from Eq (1) with \(a=teach\)
\(Q_{teach}^{t-1,t}=\sum\limits_i\big(\frac{\omega^{t-1}_{teach,i}e^{t-1}_i}{[\sum_j\omega^{t-1}_{teach,j}e_j^{t-1}]}\big)\frac{q^t_{teach,i}}{q^{t-1}_{teach,i}}\) . (7)
(ii) Grant index
The grant index follows from Eq (1) with \(a=grant\)
\(Q_{grant}^{t-1,t}=\sum\limits_i\big(\frac{\omega^{t-1}_{grant,i}e^{t-1}_i}{[\sum_j\omega^{t-1}_{grant,j}e_j^{t-1}]}\big)\frac{q^t_{grant,i}}{q^{t-1}_{grant,i}} = \sum\limits_i\big(\frac{\omega^{t-1}_{res,i}e^{t-1}_i}{[\sum_j\omega^{t-1}_{res,j}e_j^{t-1}]}\big)\frac{q^t_{grant,i}}{q^{t-1}_{grant,i}}\) , (8)
Where the second equality holds for constant \(\theta_{grant}\) across the university sector.
(iii) Completion index
Similar to (8), the completion index can be calculated from Eq (1) with \(a=comple\)
\(Q_{comple}^{t-1,t}=\sum\limits_i\big(\frac{\omega^{t-1}_{comple,i}e^{t-1}_i}{[\sum_j\omega^{t-1}_{comple,j}e_j^{t-1}]}\big)\frac{q^t_{comple,i}}{q^{t-1}_{comple,i}} = \sum\limits_i\big(\frac{\omega^{t-1}_{res,i}e^{t-1}_i}{[\sum_j\omega^{t-1}_{res,j}e_j^{t-1}]}\big)\frac{q^t_{comple,i}}{q^{t-1}_{comple,i}}\) . (9)
Where the second equality holds for constant \(\theta_{comple}\) across the university sector.
(iv) Research index
The research index is calculated as the weighted aggregate of the grant index (8) and completion index (9):
\(Q_{res}^{t-1,t}=\big(\frac{\sum_i\omega^{t-1}_{grant,i}e^{t-1}_i}{\sum_j\omega^{t-1}_{res,j}e^{t-1}_j}\big)Q^{t-1,t}_{grant}+\big(\frac{\sum_i\omega^{t-1}_{comple,i},e^{t-1}_i}{\sum_j\omega^{t-1}_{res,j}e^{t-1}_j}\big) Q^{t-1,t}_{comple}=\theta_{grant}Q^{t-1,t}_{grant}+\theta_{comple}Q^{t-1,t}_{comple}\) , (10)
where the second equality is a direct consequence of \(\theta_{grant}\) and \(\theta_{comple}\) being constant across the university sector.
(v) Total university index
A total university index is calculated as aggregate of the teaching index (7) and research index (10):
\(Q^{t-1,t}_{total}=\frac{\sum_i\omega^{t-1}_{teach,i}e^{t-1}_i}{\sum_je^{t-1}_j}Q^{t-1,t}_{teach}+\frac{\sum_1\omega^{t-1}_{res,i}e^{t-1}_i}{\sum_je^{t-1}_j}Q^{t-1,t}_{res}\). (11)
Alternatively, the following aggregate of teaching, grant, and completion leads to the same result as (11):
\(Q^{t-1,t}_{total}=\sum\limits_i\big[\big(\frac{q^t_{teach,i}}{q^{t-1}_{teach,i}}\omega^{t-1}_{teach,i}+\frac{q^t_{grant,i}}{q^{t-1}_{grant,i}}\omega^{t-1}_{grant,i}+\frac{q^t_{comple,i}}{q^{t-1}_{comple,i}}\omega^{t-1}_{comple,i}\big)\frac{e^{t-1}_i}{\sum_je^{t-1}_j}\big]\). (12)
(vi) Annually chained index
An annually chained index from \(0\) to \(t\) can be constructed from year-to-year indexes \(Q^{t-1,t}\) as
\(Q^{0,t}_{chain}=Q^{0,1}\times Q^{1,2}\times\cdots \times Q^{t-1,t}\) . (13)
Previous catalogue number
This release previously used catalogue number 5900.0.00.003