WHEN IS THE MEAN NOT A USEFUL MEASURE?
The mean is a good choice of measure of central tendency when the data is more or less symmetrically spread out from the lowest to highest values. However, the mean is not a good measure when the data is unevenly spread.
Let us take the case above, but this time change the CEO's earnings to $200,000.
Using the formula again:
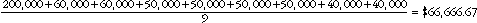
The mean income of these nine employees has increased to $66,666.
Given that only one of the nine employees earns above this amount, the mean is not a good measure of where the midpoint lies.
This is demonstrated in the diagram below.
In this case a much better measure of the midpoint would be the
median.
Print Page
Print All