TECHNICAL NOTE RELIABILITY OF THE ESTIMATES
RELIABILITY OF THE ESTIMATES
1 Since the estimates in this publication are based on information obtained from occupants of a sample of dwellings, they are subject to sampling variability. That is, they may differ from those estimates that would have been produced if all occupants of all dwellings had been included in the survey. One measure of the likely difference is given by the standard error (SE), which indicates the extent to which an estimate might have varied by chance because only a sample of dwellings (or occupants) was included. There are about two chances in three (67%) that a sample estimate will differ by less than one SE from the number that would have been obtained if all dwellings had been included, and about 19 chances in 20 (95%) that the difference will be less than two SEs.
2 Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate:
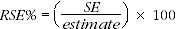
3 RSEs for estimates from 2006-07 MPHS are published for the first time in 'direct' form. Previously a statistical model was produced that relates the size of estimates to their corresponding RSEs, and this information was displayed via an 'SE table'. From this point onwards, RSEs for MPHS estimates have now been calculated for each separate estimate and published individually. The Jackknife method of variance estimation is used for this process, which involves the calculation of 30 'replicate' estimates based on 30 different subsamples of the original sample. The variability of estimates obtained from these subsamples is used to estimate the sample variability surrounding the main estimate.
4 Limited publication space does not allow for the separate indication of the SEs and/or RSEs of all the estimates in this publication, only those for Table 4.2 have been included at the end of these Technical Notes. However, RSEs for all these estimates are available free-of-charge on the ABS web site <www.abs.gov.au>, released in spreadsheet format as an attachment to this publication, Household Use of Information Technology, Australia, 2006-07 (cat. no.8146.0)
5 In the tables in this publication, only estimates (numbers, percentages, means and medians) with RSEs less than 25% are considered sufficiently reliable for most purposes. However, estimates with larger RSEs have been included and are preceded by an asterisk (e.g. *3.4) to indicate they are subject to high SEs and should be used with caution. Estimates with RSEs greater than 50% are preceded by a double asterisk (e.g. **2.1) to indicate that they are considered too unreliable for general use.
CALCULATION OF STANDARD ERRORS
6 SEs can be calculated using the estimates (counts or means) and the corresponding RSEs. For example Table 4.2 shows that the estimated number of households with Internet access in 2006-07 is 5,138,000. In the corresponding RSE table (on page 58), the RSE for this estimate is shown to be 0.6%. The SE is: 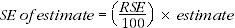 = 0.006 * 5,138,000 = 31,000 (rounded to nearest 1,000)
= 0.006 * 5,138,000 = 31,000 (rounded to nearest 1,000)
7 Therefore there are about two chances in three that the value that would have been produced if all dwellings had been included in the survey will fall within the range 5,107,000 to 5,169,000 and about 19 chances in 20 that the value will fall within the range 5,076,000 to 5,200,000.
PROPORTIONS AND PERCENTAGES
8 Proportions and percentages formed from the ratio of two estimates are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. A formula to approximate the RSE of a proportion is given below. This formula is only valid when x is a subset of y.
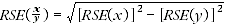
9 For example in Table 4.2 the estimate for the proportion of households in New South Wales with Broadband access in terms of those with Internet access is 68%.
10 From the RSE table on page 58 the RSE of the estimated number of households in New South Wales with Broadband access is 1.7%, and the estimated number of New South Wales households with Internet access is 0.8%.
11 Applying the above formula, the RSE of the proportion is: 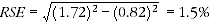
12 This then gives an SE for the proportion (68%) of (1.5/100) x 68 = 1 percentage point.
13 Therefore there are about two chances in three that the proportion of households in New South Wales with Broadband access is between 67% and 69%, and 19 chances in 20 that the proportion is within the ranges 66% and 70%.
DIFFERENCES
14 Published estimates may also be used to calculate the difference between two survey estimates (of numbers or percentages). Such an estimate is subject to sampling error. The sampling error of the difference between two estimates depends on their SEs and the relationship (correlation) between them. An approximate SE of the difference between two estimates (x-y) may be calculated by the following formula:
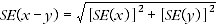
15 From table 4.2, it is estimated that 5,138,000 households accessed the Internet using a home computer in 2006-07. This estimate has a RSE of 0.6 (see Table below), which corresponds to a standard error of around 31,000 (see paragraph 6 above). The corresponding figure for 2005-06 was 4,730,000, with a standard error of around 39,000. The estimated increase in the number of households with home Internet access from the previous year is thus 408,000. Substituting the SEs for 2005-06 and 2006-07 in the above formula the SE on the movement is around 50,000. There are 2 chances in 3 that the true value is within the range 358,000 to 458,000 households and 19 chances in 20 that the true value is in the range 308,000 to 508,000 households.
16 While this formula will only be exact for differences between separate and uncorrelated characteristics or subpopulations, it is expected to provide a good approximation for all differences likely to be of interest in this publication.
SIGNIFICANCE TESTING
17 The statistical significance test for any of the comparisons between estimates was performed to determine whether it is likely that there is a difference between the corresponding population characteristics. The standard error of the difference between two corresponding estimates (x and y) can be calculated using the formula in paragraph 14. This standard error is then used to calculate the following test statistic :
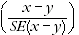
18 If the value of this test statistic is greater than 1.96 then we may say there is good evidence of a real difference in the two populations with respect to that characteristic. Otherwise, it cannot be stated with confidence that there is a real difference between the populations.
19 The imprecision due to sampling variability, which is measured by the SE, should not be confused with inaccuracies that may occur because of imperfections in reporting by respondents and recording by interviewers, and errors made in coding and processing data. Inaccuracies of this kind are referred to as non-sampling error, and they occur in any enumeration, whether it be a full count or sample. Every effort is made to reduce non-sampling error to a minimum by careful design of questionnaires, intensive training and supervision of interviewers, and efficient operating procedures.
Table 4.2: Household Internet Connection, Selected Characteristics, by Type of Access, Relative Standard Errors - 2006-07 |
|
 |  | Number of
households
accessing the
internet at home | Dial-Up | Broadband | Both | Don't
know |
 |  | % | % | % | % | % |
|
| Households |  |  |  |  |  |
 | Without children under 15 | 0.9 | 2.5 | 1.0 | 20.3 | 14.5 |
 | With children under 15 | 0.7 | 3.4 | 1.9 | 30.3 | 21.5 |
| Equivalised household income |  |  |  |  |  |
 | $0 - $39,999(a) | 1.7 | 3.2 | 1.6 | 27.0 | 15.5 |
 | $40,000 - $79,999 | 1.8 | 3.7 | 2.9 | 29.9 | 23.1 |
 | $80,000 - $119,999 | 4.5 | 8.8 | 5.4 | 42.1 | 56.2 |
 | $120,000 or over | 5.9 | 12.8 | 6.9 | 76.3 | - |
 | Could not be determined | 3.1 | 4.3 | 3.2 | 29.4 | 18.1 |
| Household income |  |  |  |  |  |
 | $0 - $39,999(a) | 2.3 | 3.9 | 2.9 | 30.0 | 23.7 |
 | $40,000 - $79,999 | 2.4 | 3.8 | 2.7 | 35.0 | 18.8 |
 | $80,000 - $119,999 | 2.3 | 5.7 | 3.7 | 36.4 | 31.3 |
 | $120,000 or over | 2.6 | 7.5 | 3.0 | 43.6 | 82.5 |
 | Could not be determined | 3.1 | 4.3 | 3.2 | 29.4 | 18.1 |
| Equivalised household income quintiles(b) |  |  |  |  |  |
 | Lowest quintile | 3.7 | 6.0 | 5.4 | 57.0 | 31.4 |
 | Second quintile | 3.4 | 6.0 | 3.4 | 33.8 | 34.4 |
 | Third quintile | 3.0 | 6.3 | 2.7 | 58.3 | 26.2 |
 | Fourth quintile | 2.2 | 5.2 | 3.6 | 40.7 | 29.5 |
 | Highest quintile | 2.8 | 6.0 | 2.8 | 29.1 | 41.9 |
| State/Territory |  |  |  |  |  |
 | New South Wales | 0.8 | 4.3 | 1.7 | 33.6 | 23.9 |
 | Victoria | 1.5 | 4.1 | 1.6 | 28.6 | 20.6 |
 | Queensland | 1.4 | 4.0 | 2.1 | 28.3 | 24.3 |
 | South Australia | 2.5 | 4.6 | 2.9 | 45.4 | 33.9 |
 | Western Australia | 1.7 | 5.1 | 2.2 | 44.2 | 28.2 |
 | Tasmania | 2.2 | 6.3 | 3.6 | 101.0 | 38.7 |
 | Northern Territory | 5.9 | 14.7 | 8.5 | 103.2 | - |
 | Australian Capital Territory | 2.4 | 12.1 | 3.2 | 57.7 | 49.2 |
| Remoteness area |  |  |  |  |  |
 | Major cities of Australia | 0.8 | 2.8 | 1.1 | 20.1 | 15.0 |
 | Inner regional Australia | 2.8 | 4.6 | 3.0 | 32.7 | 28.4 |
 | Outer regional Australia | 5.5 | 6.7 | 6.8 | 80.5 | 30.4 |
 | Remote Australia | 11.1 | 17.0 | 13.9 | 62.5 | 68.2 |
| Region |  |  |  |  |  |
 | Metropolitan areas | 0.7 | 2.7 | 1.1 | 22.0 | 13.8 |
 | Ex-metropolitan areas | 1.2 | 3.3 | 1.8 | 25.8 | 21.2 |
| Total | 0.6 | 2.2 | 0.7 | 16.5 | 12.6 |
|
| - nil or rounded to zero (including null cells) |
| (a) Includes those households with income less than zero. |
| (b) Excludes those households where income could not be determined. |
 Print Page
Print Page
 Print All
Print All