Feature Article - Why are there differences between two seasonally adjusted measures of Australian total employment?
This article was originally published in the December 1999 issue of Labour Force, Australia (cat. no. 6203.0), and the December 1999 issue of Australian Economic Indicators (cat. no. 1350.0).
INTRODUCTION
Users of seasonally adjusted estimates of employed persons, published monthly by the Australian Bureau of Statistics (ABS) in Labour Force, Australia, Preliminary (cat. no. 6202.0) and Labour Force, Australia (cat. no. 6203.0), have noted that the sum of the seasonally adjusted estimates of employed persons for the six States differs from the estimate of Australian Total Employment. The difference cannot always be explained by unpublished Territory estimates. Some users may even have noted that the differences are seasonal.
This article explains these differences in Labour Force estimates and why they can occur when the seasonal adjustment process is applied. Finally, the article describes how the differences are minimal in the published trend estimates.
HOW BIG ARE THE DIFFERENCES?
The ABS produces but does not publish seasonally adjusted estimates of Employed Persons for the Australian Capital Territory and Northern Territory. These estimates are too volatile and liable to revision to be suitable for publication. However, even if the seasonally adjusted estimates for the published State and unpublished Territory totals are added up, the result does not agree exactly with the published seasonally adjusted estimate of Employed Persons for Australia.
This difference between the month-to-month movements of the seasonally adjusted Australian Total Employed Persons and sum of the States and Territories, starting from January 1995, is shown in graph 1. The difference has been as much as plus or minus 20,000 persons in the last few years and, as evidenced by the graph, there is a consistent pattern that repeats every twelve months, notably in month-to-month movements from January to February, from February to March, from July to August and from August to September each year. In other words, the pattern is seasonal.

WHY ARE THERE DIFFERENCES AND WHY ARE THEY SEASONAL?
We now turn to why there are differences between the two seasonally adjusted estimates of the same quantity, using the employment series to illustrate, and why these differences are seasonal.
The X11 seasonal adjustment procedure
In order to produce seasonally adjusted estimates, the ABS uses a modified version of the US Bureau of the Census X11 procedure, the procedure most widely used by statistical agencies around the world. Central to the X11 procedure is the concept of time series decomposition, whereby the original series is viewed as being the result of the combined action of three distinctly different notional influences. These are:
- the trend;
- systematic calendar related effects; and
- residual/irregular variation.
The X11 procedure takes the original series and estimates the three components. The component consisting of systematic calendar related effects is then removed from the original data to produce the seasonally adjusted series. An alternative way of viewing the seasonally adjusted series is to regard it as a combination of the trend and residual/irregular variation.
In the case of Labour Force Employment statistics, employment in the economy varies from one month to the next in a systematic way throughout the year. For example, in the Retail sector there is increased employment in November and December each year as shops take on additional staff to cope with the busy Christmas shopping period. Conversely, many manufacturing businesses close for annual holidays during January which reduces employment in that month. These seasonal fluctuations in employment are the systematic calendar related effects which are removed by the seasonal adjustment of Labour Force Employment statistics.
To estimate the seasonal variation in employment, X11 estimates and then removes an initial estimate of the trend component from the original data to produce a series which contains only seasonal and residual/irregular variation. The reason for removing the trend is so that the remaining seasonal-irregular series will display an essentially unchanging level over its whole span. Next the seasonal-irregular values are grouped together by month so that all the January observations end up in one group, all the February observations end up in a second group, and so on for the other months. Within each group the observations are arranged in a yearly sequence, starting with the observation from the earliest year spanned by the time series and ending with the observation from the most recent year.
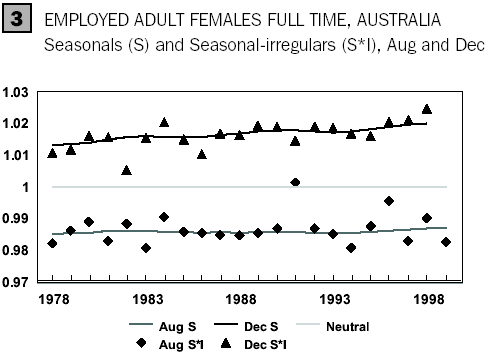
Each sequence is then smoothed using a ‘seasonal moving average’. The values being smoothed contain only seasonal and residual/irregular variation (since the trend has already been removed), and applying a moving average smoothes away the rapidly fluctuating residual/irregular component to leave only the slowly varying seasonal component. An example of the effect of this process is contained in graph 3. The triangles show the individual seasonal-irregulars (S*I) for each December month from 1978 to 1998 and the smooth line passing near the triangles is the seasonal factor for December month. The graph shows how the seasonal factor for December has gradually changed over the years, as shopping patterns have altered. Similarly, the diamonds show the seasonal-irregulars for the month of August. In this way it is possible to obtain an estimate of the seasonal level of employment for each month while still allowing for the fact that the seasonal level may be changing gradually over time. The X11 procedure allows for the selection of different seasonal moving averages depending on the particular characteristics of the series being analysed.
DERIVING SEASONALLY ADJUSTED EMPLOYED PERSONS ESTIMATES
The ABS derives its published seasonally adjusted estimates for Employed Persons for Australia and the States by directly seasonally adjusting all component series before adding them up to produce seasonally adjusted estimates of the corresponding Totals. There are several different ways in which the Australia and State Total series could be derived. For example, one way of deriving the Total Employed Persons series is to add Full Time Employed Persons and Part Time Employed Persons. Another way of obtaining Total Employed Persons is to add Junior and Adult Employed Persons. A third option is to add Male and Female Employed Persons, and a fourth is to add Employed Persons for the States and Territories to get the Australia Total series.
Seasonal adjustment could in theory be undertaken at a very fine component level, for example NSW Junior Full Time Employed Males might be seasonally adjusted and added to similarly disaggregated series to obtain a total. However, the quality of the adjustments tends to decline as the series are broken down into finer level components, and if the seasonal adjustment of disaggregated splits is attempted at too low a level the results are so unreliable as to be of little use.
The reason for this is that the seasonal pattern which is estimated and then removed by the seasonal adjustment process may be regarded as a signal which is mixed with an irregular or noise element. The noise element consists of a series of random fluctuations which have a tendency to cancel to a degree when component series are added together. More aggregated series usually have a better signal-to-noise characteristic than the contributing component series, which enables a more accurate estimate of the seasonality to be made.
The optimal level for fitting the seasonal moving average will vary with the characteristics of the series. For key series, such as Employed Persons for Australia, the ABS assesses the appropriate level at which to seasonally adjust components. Total Employed Persons Australia is built up from six component series which are directly adjusted. The six series are Adult Females Employed Full Time, Adult Males Employed Full Time, Junior Females Employed Full Time, Junior Males Employed Full Time, Females Employed Part Time, and Males Employed Part Time. Each individual State Total is formed by the addition of two directly adjusted component series: Employed Females in that State and Employed Males in that State.
A directly seasonally adjusted total series will not, in general, equal the sum of individually seasonally adjusted component series. One reason for the difference relates to the way that unusual or extreme seasonal-irregulars in a series are replaced with a weighted average of nearby values which are regarded as being more typical. When component series are aggregated, extreme seasonal-irregular values of opposite sign can cancel each other out, leading to a different interpretation of which values are to be treated as extreme at the more aggregated level.
Another possible source of discrepancy arises from the parameter settings that are employed for the seasonal adjustment of the different series. Such parameter settings include the choice of which seasonal and trend moving averages are to be used. The settings are normally chosen individually for each series. It can easily happen that various component series use different parameter settings for their adjustment. For example, if two component series are individually seasonally adjusted, one component may be adjusted using a seven term seasonal moving average while the other component is adjusted using an eleven term seasonal moving average. If the two components are added together to form a total and then seasonally adjusted, whichever seasonal moving average is used on the total must differ from the seasonal moving average applied to at least one of the components. The settings chosen for other adjustment parameters can cause similar problems.
We can now see why differences between seasonally adjusted estimates of the same data adjusted at different levels of aggregation are an expected consequence of the seasonal adjustment process. The question remains as to why these differences are seasonal.
WHY ARE THE DIFFERENCES SEASONAL?
There is an inbuilt constraint in the seasonal adjustment process which causes the differences between two seasonally adjusted estimates of the same quantity to be seasonal. The constraint is that, for monthly series, the estimated seasonal adjustment factors sum to approximately twelve over any twelve month period. This step is designed to ensure that the level of the seasonally adjusted series does not differ appreciably from the level of the unadjusted series over the long run.
As a consequence, whenever the seasonal adjustment factors for a particular month differ slightly, depending on whether the seasonal adjustment process is applied to the total series or to each component series, there must be a corresponding difference in another month or months going in the opposite direction so that the factors will sum to approximately twelve in both cases. For example, if the implied seasonal adjustment factor for January for the Australia Total series is somewhat higher than the corresponding factor for the sum of State Totals, then there must be other months such as February and August where the implied factor for the Australia Total series is lower than for the Sum of State Totals.
The use of seasonal moving averages to estimate the seasonality for each month allows the seasonal patterns to evolve in a smooth and slowly varying fashion over the years. This produces estimates of the seasonality in each month for adjacent years that are quite similar. When this is combined with the inbuilt constraint in the seasonal adjustment process, we find that differences between two different seasonally adjusted estimates of the same quantity show a seasonal pattern.
TREND ESTIMATES
The time series decomposition view of the seasonal adjustment process implies that a seasonally adjusted series contains both the trend and residual-irregular variation. The ABS produces trend estimates for monthly series by smoothing the seasonally adjusted series with a 13 term Henderson moving average to remove the residual-irregular variation. Residual-irregular variation is often regarded as little more than statistical ‘noise’. By removing it, the original data series is decomposed into only one notional influence, the trend.
Focusing on the trend estimates confers two advantages from the perspective of the problem under discussion. Graph 4 shows the difference in month-to-month movements between the trend Australian Total and the sum of all State and Territory Totals. In contrast to Graph 1 where the same differences are given for the seasonally adjusted series, an immediate reduction in the size of the differences between month-to-month movements can be seen. The maximum differences in month-to-month movements between the trend estimates for the Australian Total and the sum of State Totals are around plus or minus 2,000 persons, whereas for the seasonally adjusted series the maximum differences are around plus or minus 20,000 persons.
A second benefit of using trend estimates rather than seasonally adjusted estimates is that trend estimates of Employed Persons are published for all the States and Territories.
CONCLUSION
In conclusion, in order to get the best possible seasonally adjusted series, it is appropriate to optimise the level of aggregation at which the procedures are applied. However, whenever two seasonally adjusted estimates of the same underlying quantity are obtained by adding components that have been adjusted at different levels of aggregation, differences are to be expected. Furthermore, when the X11 procedure is used, the differences will show a seasonal pattern. The size of the differences will be appreciably smaller when trend estimates rather than seasonally adjusted estimates are used. Trend estimates can offer other advantages to the users including greater data availability, and since trend estimates are free from the masking effect of unwanted statistical noise, they are generally more suitable for most business decisions and policy advice.
FURTHER INFORMATION
For more information, please contact the Assistant Director, Labour Force Estimates on Canberra 02 6252 6565.
For email enquiries, please contact Client Services on client.services@abs.gov.au.
 Print Page
Print Page