TECHNICAL NOTE
RELIABILITY OF THE ESTIMATES
1 As the estimates in this publication are based on information obtained from a sample of persons, they are subject to sampling variability. That is, the estimates may differ from those that would have been produced had all persons been included in the survey.
2 One measure of the likely difference is given by the standard error estimate (SE), which indicates the extent to which a sample estimate might have varied by chance because only a sample of persons was included. There are about two chances in three (67%) that a sample estimate will differ by less than one SE from the population parameter that would have been obtained if all persons had been surveyed, and about 19 chances in 20 (the 95% confidence level) that the difference will be less than two SEs.
3 Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate.

4 RSEs for all estimates have been calculated using the Jack-knife method of variance estimation. This involves the calculation of 60 'replicate' estimates based on 60 different sub-samples of the obtained sample. The variability of estimates obtained from these sub-samples is used to estimate the sample variability surrounding the estimate.
5 The Excel spreadsheets (in Downloads Tab) contain all the tables produced for this release and the calculated RSEs for each of the estimates.
6 Indications of the level of sampling error in this survey are measured by Relative Standard Errors (RSEs). Estimates with a relative standard error (RSE) of less than 25% are considered sufficiently reliable for most purposes, and only estimates of such precision are referred to in the text of this release (unless otherwise noted). Due to the relatively small numbers of persons experiencing certain types of violence, some of the estimates provided within the data cubes are subject to very high sampling error.
7 Estimates of counts and proportions/percentages with an RSE of 25% to 50% are preceded by a single asterisk (e.g. *3.4) to indicate the estimate or proportion should be used with caution. Estimates of counts and proportions/percentages with RSEs greater than 50%, annotated by a double asterisk (e.g. **0.6), are considered too unreliable for general use.
CALCULATION OF STANDARD ERROR
8 Standard errors can be calculated using the estimates (counts or percentages) and the corresponding RSEs. For example, the estimated number of women who experienced violence in the last 12 months was 467,300. The RSE corresponding to this estimate is 5.9%. The SE is calculated by:
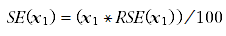
= (467,300*5.9) / 100
= 27,600 (rounded to the nearest 100)
CONFIDENCE INTERVAL
9 There are about two chances in three that the sample estimate will differ by less than one SE from the population parameter that would have been obtained if all dwellings had been included in the survey, and about 19 chances in 20 that the difference will be less than two SEs. This example is illustrated in the diagram below.

PROPORTIONS AND PERCENTAGES
10 Proportions and percentages, which are formed from the ratio of two estimates, are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. For proportions where the denominator is an estimate of the number of persons in a grouping and the numerator is the number of persons in a sub-group of the denominator group, the formula for an approximate RSE is given by:
![Equation: RSE (x / y) = square root of ([RSE (x)] squared - [RSE (y)] squared)](/ausstats/abs@.nsf/0/f72bd8b94c534be3ca2581d1000c3945/Body/0.34F8!OpenElement&FieldElemFormat=gif)
DIFFERENCES
11 The difference between two survey estimates (counts or percentages) is also subject to sampling error. An approximate SE of the difference between two estimates (x-y) may be calculated by the formula:

12 This approximation can generally be used whenever the estimates come from different samples, such as two estimates from different years, or two estimates for two non-intersecting subpopulations in the one year. If the estimates come from two populations, one of which is a subpopulation of the other, the standard error is likely to be lower than that derived from this approximation.
SIGNIFICANCE TESTING
13 All differences and changes mentioned have been tested for statistical significance with a 95% level of confidence that there is a real difference in the two populations being tested. To determine whether there is a statistical difference between any other two estimates significance testing should be undertaken.
14 A statistical significance test for a comparison between estimates can be performed to determine whether it is likely that there is a difference between the corresponding population characteristics. The standard error of the difference between two corresponding estimates (x and y) can be calculated using the formula shown above in the Differences section. This standard error is then used to calculate the test statistic:

15 If the value of this test statistic is greater than 1.96 then there is good evidence, with a 95% level of confidence, of a statistically significant difference in the two populations with respect to that characteristic. Otherwise, it cannot be stated with confidence (at the 95% confidence level) that there is a real difference between the populations.
16 Tables which show rates from 2005 and 2012 have been tested to determine whether changes over time are statistically significant. Significant differences have been annotated. In all other tables which do not show the results of significance testing, users should take account of the sample error when comparing estimates for different populations.
17 Most of the tables in this release also provide information to show men's and women's experience of violence. Significant differences have been noted in the commentary. Where there is no associated commentary for tables (not all tables have been noted in the commentary), users should take account of the sample error when comparing estimates between men and women or when comparing estimates for different populations.
Example of estimates where there was a statistically significant difference
18 An estimated 8.7% of all men aged 18 years or over and 5.3% of all women aged 18 years or over had experienced violence during the 12 months prior to the survey (refer Table 1).
- The estimate of 8.7% of men who had experienced violence in the 12 months prior to the survey has an RSE of 7.4%. There are 19 chances out of 20 that an estimate of between 7.4% and 10.0% of men would have been obtained if all dwellings had been included in the survey.
- The estimate of 5.3% of women who had experienced violence in the 12 months prior to the survey has an RSE of 5.9%. There are 19 chances out of 20 that an estimate of between 4.7% and 5.9% women would have been obtained if all dwellings had been included in the survey.

- The value of the test statistic (using the formula shown in paragraph 14) is 4.75
19 As the value of this test statistic, at 4.75, is greater than 1.96, this showed there was evidence, with a 95% level of confidence, of a statistically significant difference in the two estimates. By calculating the confidence interval for the proportion of men and women who experienced violence in the 12 months prior to the survey, it can be seen that the confidence intervals for estimates for men and women do not overlap (where the confidence intervals do not overlap there is always a statistically significant difference). Therefore there is evidence to suggest that men were more likely than women to have experienced violence in the 12 months prior to the survey.
 Print Page
Print Page
 Print All
Print All