4530.0 - Crime Victimisation, Australia, 2016-17

ARCHIVED ISSUE Released at 11:30 AM (CANBERRA TIME) 16/02/2018

Page tools: Print Page Print All
Explanatory Notes Glossary Abbreviations Quality Declaration Data Quality (Technical Note)	TECHNICAL NOTE Reliability of the estimates 1 The estimates in this publication are based on information obtained from a sample survey. Errors in data collection or processing, known as non-sampling error, can impact on the reliability of the resulting statistics. In addition, estimates based on sample surveys are subject to sampling error. That is, the estimates may differ from the true value of the characteristics being measured that would have been obtained had all persons in the population been included in the survey. Non-sampling error 2 Non-sampling error may occur in any statistical collection, whether it is based on a sample or a full count such as a census. Sources of non-sampling error include non-response, errors in reporting by respondents or recording of answers by interviewers, and errors in coding and processing data. Every effort is made to reduce non-sampling error by careful design and testing of questionnaires, training and supervision of interviewers, and extensive editing and rigorous quality control procedures at all stages of data processing. Sampling error 3 Sampling error refers to the difference between an estimate obtained from surveying a sample of persons, and the true value of the characteristic being measured that would have been obtained if the entire in-scope population was surveyed. Sampling error can be measured in a standardised way using Standard Error (SE) calculations, which indicates the extent to which an estimate might have varied by chance because only a sample of persons was surveyed. There are about two chances in three (67%) that a sample estimate will differ by less than one SE from the number that would have been obtained if all persons had been surveyed, and about 19 chances in 20 (95%) that the difference will be less than two SEs. For more details see What is a Standard Error and Relative Standard Error, Reliability of estimates for Labour Force data. 4 In this publication, the standard error of the estimate is given as a percentage of the estimate it relates to, known as the relative standard error (RSE). 5 The Excel files available from the Downloads tab contain all the tables produced for this release, including all estimates and their corresponding RSEs. 6 Only estimates (numbers or percentages) with an RSE of less than 25% are considered sufficiently reliable for most analytical purposes. However, estimates with an RSE over 25% have also been included. Estimates with an RSE in the range 25% to 50% are less reliable and should be used with caution, while estimates with an RSE greater than 50% are considered too unreliable for general use. All cells in the publication tables containing an estimate with an RSE of 25% or over are marked with asterisks, indicating whether the RSE of the estimate is in the range 25 to 50% (single asterisk ) or is greater than 50% (double asterisk ). Calculation of Standard Error* 7 Standard error (SE) can be calculated using the estimate (count or percentage) and the corresponding RSE. 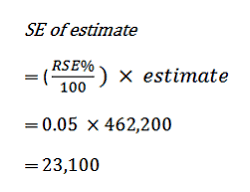For example, if the estimated number of persons who experienced physical assault in the last 12 months was 462,200, with a corresponding RSE of 5.0%, the SE (rounded to the nearest 100) is calculated by: 8 Therefore, there is about a two in three chance that the true value, which would have been obtained had all persons been included in the survey, falls within the range of one standard error below to one standard error above the estimate (439,100 to 485,300), and about a 19 in 20 chance that the true value falls within the range of two standard errors below to two standard errors above the estimate (416,000 to 508,400). This example is illustrated in the diagram below: Proportions and Percentages 9 Proportions and percentages formed from the ratio of two estimates are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. A formula to approximate the RSE of a proportion is given below. This formula is only valid when x is a subset of y: 10 As an example, if 86,600 persons experienced physical assault by an intimate partner, representing 30% of all persons who experienced physical assault by a known person (293,600); and if the RSE for the number of persons experiencing physical assault by an intimate partner is 7.7% and the RSE for the number of persons experiencing physical assault by a known person is 6.7%; then, applying the above formula, the RSE of the proportion is: 11 Using the formula given in technical note 9 above, the standard error (SE) for the proportion of persons who experienced physical assault by an intimate partner (as a proportion of those who experienced physical assault by a known person) is 1.1% (0.038 x 29.5). Hence, there are about two chances in three that the true proportion of persons who experienced physical assault by an intimate partner (as a proportion of those who experienced physical assault by a known person) is between 28.4% and 30.6%, and 19 chances in 20 that the true proportion is between 27.3% and 31.7%. Differences 12 Standard error can also be calculated on the difference between two survey estimates (counts or percentages). The standard error of the difference between two estimates is determined by the individual standard errors of the two estimates and the relationship (correlation) between them. An approximate standard error of the difference between two estimates (x,y) can be calculated using the following formula: 13 While this formula will only be exact for differences between separate and uncorrelated characteristics or sub populations, it provides a good approximation for the differences likely to be of interest in this publication. Significance Testing 14 The difference between two survey estimates can be tested for statistical significance, in order to determine the likelihood of there being a real difference between the populations with respect to the characteristic being measured. The standard error of the difference between two survey estimates (x and y) can be calculated using the formula shown above in technical note 12. This standard error is then used in the following formula to calculate the test statistic: 15 If the value of the test statistic is greater than 1.96 then this supports, with a 95% level of confidence, a real (i.e. statistically significant) difference between the two populations with respect to the characteristic being measured. If the test statistic is not greater than 1.96, it cannot be stated with a 95% level of confidence that there is a real difference between the populations with respect to that characteristic. 16 Annual changes between 2015-16 and 2016-17 in victimisation rates, comparisons between state and territory estimates to national estimates for 2016-17, reporting rates, and the proportion of persons believing alcohol or any other substance contributed to their most recent incident of physical assault and face-to-face threatened assault, have been tested to determine whether the change/difference is statistically significant. Significant differences have been annotated with a cell comment. In all other tables which do not show the results of significance testing, users should take RSEs into account when comparing estimates for different populations, or undertake significance testing using the formula provided in technical note 14 to determine whether there is a statistically significant difference between any two estimates. Changes in Crime Victimisation Rates Over Time 17 Changes in crime victimisation rates over time have been examined by fitting functions to the time points of data for each crime type. The function of best fit was selected based on the highest R-squared value. R-squared is a measure of how well the fitted model explains the variance of the dependant variable (i.e. the crime type). The closer R-squared is to 1.0, the better the function fits the data points. 18 For the modelled data presented in this publication, only fitted functions with a R-squared value greater than 0.7 have been included. Whilst the R-squared has limitations, particularly in the context of non-linear models, it is still a useful indicator of model fit. 19 The functions used to analyse patterns of change in national victimisation rates over time have not taken into account the survey error associated with the annual victimisation rates. This is expected to have a negligible impact on the analysis, as the survey error is small. 20 The functions used to analyse patterns of change in state/territory victimisation rates over time have not taken into account the survey error associated with the annual victimisation rates, and fitted functions have only been included where the following criteria were met: Survey estimates for the victimisation rate had a relative standard error (RSE) of 25% or less. The fitted function was within the 95% confidence interval for the victimisation rate and had an R-squared value of 0.7 or above. Back to the top Document Selection These documents will be presented in a new window.