MULTILATERAL METHODS
BACKGROUND
2.1 Multilateral methods possess a number of desirable qualities, both theoretical and practical, to produce temporal price indexes from big data sources. The theoretical qualities include maintaining transitivity when reweighting and chaining frequently; while, from a practical perspective, automated processes allow a greater sample of products to be used to produce price indexes.
2.2 The international price statistics community has reached a consensus that multilateral methods are the most appropriate approach to produce temporal price indexes when using big data (UNECE 2016). At this point in time no specific multilateral method has received international endorsement. Over recent years researchers have been proposing several multilateral methods for producing temporal indexes. As described by de Haan (2015, p.1), "in spite of all the research that has been done, so far only a handful of countries have actually implemented scanner data into their CPI [...] using different methods and practices." This reticence in implementation and divergence in methods and practice stems from a number of factors, including a lack of consensus amongst researchers or leading NSOs about the best method to use, and the circumstances in which each NSO produces their CPI.
2.3 The difference between the multilateral methods themselves is in the aggregation approach each takes. For instance, the TPD method uses a regression based approach that estimates price change over time by measuring the statistical relationship between prices, products and time. The GK and Quality Adjusted Unit Value (QAUV) methods in general use a unit value approach to estimate price change and so necessitate product homogeneity to be able to standardise the quantities into common units. The difference between the QAUV_TPD and GK is in the approach to standardising the quantities - these will be discussed in this section. The GEKS method applies a geometric mean of the ratios of all bilateral indexes.
2.4 This section describes the multilateral methods the ABS is investigating for future implementation in the CPI. The choice of index formula, in part, depends on the transactions datasets that are available to the NSO. The transactions data used in this publication(footnote 1) contain the following generic data fields: city, date, SKU, product description, proprietor classifications, quantity and value sold of each product. Due to the lack of detailed product characteristics available in the data, this publication focuses on a selection of popular matched-model multilateral methods including the TPD, GK, QAUV and GEKS methods (footnote 2) .
TPD
2.5 The TPD method uses a regression approach that is similar to hedonic based methods previously used in the Australian CPI - it uses the statistical relationship between prices, products and time to directly estimate price change over time. The TPD method is a technique adapted by Aizcorbe, Corrado and Doms (2003) from the Country Product Dummy (CPD) method for spatial comparisons.
2.6 The TPD model is estimated by pooling together data for a specified window length (T+1) and modelling the log of price against time and product binary indicators. The TPD model is expressed as:
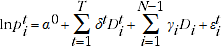 (2.1)
(2.1)
where,
 = log of price for item
= log of price for item  in period
in period 
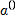 = intercept term
= intercept term
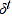 = time parameter corresponding to time period
= time parameter corresponding to time period 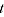
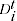 = time dummy variable, equal to 1 if the price observation
= time dummy variable, equal to 1 if the price observation 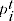 pertains to period
pertains to period 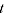 and 0 otherwise
and 0 otherwise
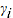 = product parameter corresponding to product
= product parameter corresponding to product 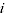
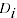 = product dummy variable, equal to 1 if the price observation
= product dummy variable, equal to 1 if the price observation 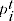 pertains to item
pertains to item 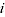 and 0 otherwise
and 0 otherwise
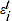 = error term
= error term
2.7 The time effect 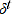 reflects the overall price level in period
reflects the overall price level in period 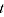 relative to a reference period 0, while the product effect
relative to a reference period 0, while the product effect 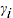 reflects the typical price of product
reflects the typical price of product 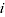 relative to the reference product N. Transforming equation 2.1, the predicted prices are
relative to the reference product N. Transforming equation 2.1, the predicted prices are 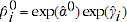 and
and 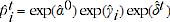 for all products belonging to an EC. Using the ratio of these predicted prices, the price index can be directly estimated from the modelled time effect parameters as follows:
for all products belonging to an EC. Using the ratio of these predicted prices, the price index can be directly estimated from the modelled time effect parameters as follows:
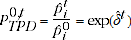 (2.2)
(2.2)
where,
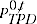 = price movement between periods 0 and
= price movement between periods 0 and 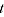
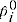 = predicted price of product
= predicted price of product 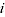 from period 0
from period 0
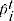 = predicted price of product
= predicted price of product 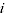 from period
from period 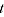
2.8 The model specified in equation 2.1 does not produce a weighted price index using ordinary least squares estimation. In order to produce a weighted price index, expenditure shares for each product 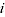 and time period
and time period  are derived and used in fitting a weighted least squares version of equation 2.1, such that the following sum is minimised:
are derived and used in fitting a weighted least squares version of equation 2.1, such that the following sum is minimised:
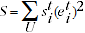 (2.3)
(2.3)
where,
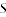 = weighted sum of squared residuals
= weighted sum of squared residuals
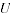 = set of all price observations in the window
= set of all price observations in the window
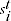 = expenditure share of product
= expenditure share of product 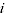 relative to other products sold in time period
relative to other products sold in time period 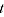
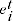 = residual error term of price observation
= residual error term of price observation 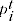
QAUV AND GK
2.9 The QAUV and GK methods both appeal to the notions of homogeneity and unit values by expressing the quantity of products into common units, then calculating a unit value across all products. The QAUV and GK have different methods of standardising quantities, these are discussed in more detail below.
2.10 The QAUV method can be described as constructing an implicit price index using information on value and quantity available from transactions datasets. The idea behind the QAUV method is to separate products into relatively homogeneous groupings, and calculate implicit price indexes by dividing a value index by a quantity index. This is expressed as:
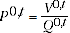 (2.4)
(2.4)
where,
 = unit value index between periods 0 and
= unit value index between periods 0 and 
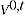 = value index between periods 0 and
= value index between periods 0 and 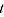
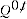 = quantity index between periods 0 and
= quantity index between periods 0 and 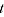
2.11 While 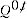 in equation 2.4 is constructed across a group of homogeneous products, it is likely that some differences in quality between individual products remain. In order to produce a standardised quantity index, each item within the homogeneous grouping can be standardised with respect to an arbitrary base item, then aggregated to produce a quantity aggregate. As a result, the standardised quantity index can be expressed as:
in equation 2.4 is constructed across a group of homogeneous products, it is likely that some differences in quality between individual products remain. In order to produce a standardised quantity index, each item within the homogeneous grouping can be standardised with respect to an arbitrary base item, then aggregated to produce a quantity aggregate. As a result, the standardised quantity index can be expressed as:
 (2.5)
(2.5)
where,
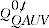 = standardised quantity index
= standardised quantity index
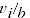 = adjustment factor comparing item
= adjustment factor comparing item 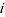 to base item
to base item 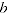
 = quantity of item
= quantity of item 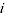 in period
in period 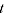
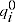 = quantity of item
= quantity of item 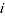 in period 0
in period 0
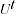 = sample of products from period
= sample of products from period 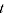
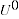 = sample of products from period 0
= sample of products from period 0
Substituting the quantity index derived in equation 2.5 into equation 2.4, the QAUV method can be expressed as:
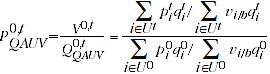 (2.6)
(2.6)
2.12 The expression in equation 2.6 does not explicitly describe a suitable method to calculate the adjustment factors 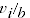 .This publication investigates two methods for calculating adjustment factors. Firstly, the method proposed by Chessa (2016) is investigated which is a temporal adaption of the GK method used to construct spatial price indexes, where adjustment factors are estimated using an iterative approach based on two sets of simultaneous equations. The adjustment factor is the quantity weighted average of deflated prices and can be expressed as:
.This publication investigates two methods for calculating adjustment factors. Firstly, the method proposed by Chessa (2016) is investigated which is a temporal adaption of the GK method used to construct spatial price indexes, where adjustment factors are estimated using an iterative approach based on two sets of simultaneous equations. The adjustment factor is the quantity weighted average of deflated prices and can be expressed as:
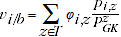 (2.7)
(2.7)
where,
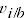 = weighted average of deflated prices of product
= weighted average of deflated prices of product 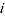
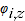 = quantity share of product
= quantity share of product 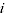 in time period
in time period 
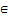

 = price of product
= price of product 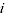 in time period
in time period 
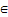
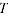
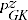 = price index in time period
= price index in time period 
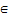
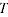
The quantity share component from equation 2.7 is derived as:
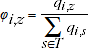 (2.8)
(2.8)
where,
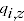 = quantity of product
= quantity of product 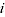 in period
in period 
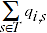 = total quantity of product
= total quantity of product 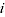 over all time periods
over all time periods 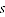
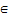
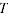
In this publication, we denote the use of quality adjustment factors as defined above for the QAUV method as GK.
2.13 An alternative option for calculating adjustment factors is the TPD approach outlined in de Haan (2015). The TPD method uses the regression model specified earlier in equation 2.1, which estimates the predicted prices 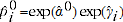 and
and 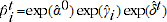 for all products. In order to express quantities in constant units, the predicted prices for all products can be compared to a base item, such that the adjustment factor becomes the following:
for all products. In order to express quantities in constant units, the predicted prices for all products can be compared to a base item, such that the adjustment factor becomes the following:
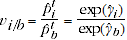 (2.9)
(2.9)
where,
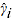 = product parameter corresponding to product
= product parameter corresponding to product 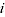
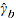 = product parameter corresponding to product
= product parameter corresponding to product 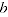
The TPD approach is denoted in a way to form adjustment factors for QAUV as QAUV_TPD.
GEKS
2.14 The GEKS method takes the geometric mean of the ratios of all bilateral indexes (calculated using the same index number formula) between a number of entities. For spatial indexes these entities are generally countries, while for price comparisons across time, the entities are time periods.
2.15 The bilateral index formula chosen for this publication is the Törnqvist index which can be expressed as:
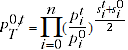 (2.10)
(2.10)
where,
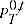 = Törnqvist index between periods 0 and
= Törnqvist index between periods 0 and 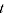
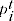 = price of item
= price of item 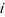 in period
in period 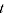
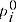 = price of item
= price of item 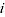 in period 0
in period 0
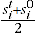 = average expenditure share item
= average expenditure share item 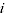 across periods 0 and
across periods 0 and 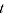
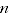 = number of matched items between periods 0 and
= number of matched items between periods 0 and 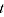
2.16 The GEKS is calculated as the geometric mean of the ratios of all matched-model bilateral indexes  and
and 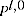 where each period
where each period 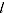 is taken in turn as the base (de Haan 2015). The GEKS method can be expressed as:
is taken in turn as the base (de Haan 2015). The GEKS method can be expressed as:
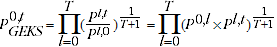 (2.11)
(2.11)
where,
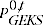 = GEKS index between periods 0 and
= GEKS index between periods 0 and 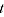
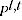 = Törnqvist index between periods
= Törnqvist index between periods 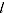 and
and 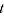
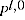 = Törnqvist index between periods
= Törnqvist index between periods  and 0
and 0
In this publication we denote the use of the Törnqvist bilateral formula to form GEKS indexes. This is referred to as GEKS indexes in the following sections.
1 See Attachment 1 of ABS (2015) for a full list of ECs where transactions data is available. <back
2 See de Haan, Willenborg and Chessa (2016) for a more exhaustive list of multilateral methods available for temporal aggregation. <back
 Print Page
Print Page
 Print All
Print All