|
|
Contents >>
Chapter 10: Volume and price measures
Chain volume measures
Introduction
10.1 Chain volume measures were introduced into the Australian national accounts in 1998. They were first presented as experimental measures for the expenditure components of GDP in the December quarter 1997 issue of Australian National Accounts: National Income, Expenditure and Product (Cat. no. 5206.0), and were an addition to the long-standing constant price estimates which were still the 'official' volume estimates. Subsequently, in the September quarter 1998 issue of Cat. no. 5206.0, the constant price estimates of both the expenditure and production components of GDP were replaced with chain volume measures from the September quarter 1986, and they became the ABS's 'official' volume estimates.
10.2 The reason for having either chain volume or constant price estimates in the national accounts is to provide time series of expenditure and production aggregates which are free of the direct effects of price change. All the current price aggregates of expenditure and production appearing in the national accounts are estimates of the sums of the values of individual transactions. Each of these transactions has two components: a price and a quantity. From one period to another the quantities and prices comprising the transactions change. This means that when the current price value of an aggregate, such as GDP, in one period is compared with the current price value in another period the difference between them usually reflects both changes in quantity and changes in price of the constituent transactions. In order to estimate by how much the 'volume' of GDP has changed between the two periods we need to measure the value of GDP in each period using the same unit prices.
10.3 For many years the ABS derived constant price estimates as a means of measuring changes in the volumes of aggregates. Constant price estimates are derived by fixing the unit prices of goods and services to those of some base year. These base year unit prices are effectively the weights used to combine the quantities of the different goods and services purchased or produced. The unit prices of different goods and services tend to grow at different rates - some at dramatically different rates, e.g. the prices of computer equipment are estimated to have declined by about 75 per cent between 1989-90 and 1997-98, while the prices of most other goods and services have increased. Therefore, over time, the price relativities of some goods and services change appreciably. This adversely affects the usefulness of constant price estimates for periods distant from the base year, and implies that the base year used to derive constant price estimates needs to be changed from time to time. It used to be ABS practice, in common with many other national statistical agencies, to change the base year every five years. However, it has been found that rebasing every five years is commonly insufficient, and SNA93 recommends rebasing every year and linking the resulting indexes to form annually reweighted chain volume measures. ABS analysis of Australian data has confirmed the need to adopt annually reweighted chain volume measures.
10.4 The decision to replace all of the ABS's constant price estimates with chain volume measures was announced on 19 March 1998 in the Information Paper: Introduction of Chain Volume Measures in the Australian National Accounts (Cat. no. 5248.0). That paper describes what chain volume measures are, their advantages and disadvantages with respect to constant price estimates, the advantages and disadvantages of different chain volume formulae, and the results of an empirical analysis.
The chaining method
10.5 There are many different ways of compiling a chain volume measure. The essential features of the ABS chain volume measures are as follows:
- Annual chain volume estimates are derived using the Laspeyres formula. Under this formula, year-to-year volume indexes of an aggregate are derived by expressing the value of the aggregate in each pair of consecutive years in the prices of the earlier year, and then dividing the value for the later year by the value for the earlier year. This is equivalent to weighting together the year-to-year volume indexes of the elementary components of the aggregate with the current price values of the earlier year. A year-to-year Laspeyres volume index at time t is given by:
- The year-to-year indexes are compounded to form a long, continuous time series, which is then referenced to the current price value of the latest base year, i.e. the second last year for which there is an annual value. In general, chain volume estimates are not additive, i.e. the accounting relationships that apply to current price data do not generally apply to their chain volume counterparts. Only the values in the reference year and the following year are additive. So by ensuring that the latest base year coincides with the reference year, the ABS approach ensures additivity for the latest two years. An annual chain Laspeyres volume measure in year t,
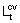 , is given by: , is given by:
- Similarly, quarter-to-quarter indexes are derived from quarterly data expressed in the prices of the previous year. These are compounded to form a long, continuous time series, which is then benchmarked (described below) to the annual chain volume series.
10.6 The steps to be followed in compiling annually reweighted chain Laspeyres volume measures for a quarterly series are best illustrated using an example. Set out below are the steps to be followed for household final consumption expenditure (HFCE). Assume that there are n financial years of data to be linked, t =1 to n.
- Step 1: For each of the 89 elemental components for each State (a total of 712 components) derive volume estimates in the prices of year t-1 for the five quarters from June quarter year t-1 to June quarter year t for years 2 to n-1. For the quarters of the final, incomplete year, year n, derive the estimates in the prices of year n-2.
- Step 2: Sum all 712 components in each time period.
- Step 3: Calculate quarter-to-quarter indexes of the aggregate. For each year t up to year n-2, the indexes from September quarter to December quarter, December quarter to March quarter and March quarter to June quarter are calculated at year t-1 prices, but the following June quarter to September quarter index is calculated at year t prices. For year n-1 and the final, incomplete year, year n, all quarter-to-quarter indexes are calculated at year n-2 prices.
- Step 4: Compound the quarter-to-quarter indexes to form a chain index.
- Step 5: Benchmark the quarterly, annually reweighted chain Laspeyres volume index of HFCE to the annual Laspeyres chain volume index referenced to the annual current price value in the reference year.
10.7 All aggregates are formed in this way with the exception of Changes in inventories. The procedure produces unsatisfactory results for this aggregate, and so chain volume measures are derived for inventory levels which are then differenced to produce volume measures of changes in inventories. The normal procedure is followed for changes in inventories when it is incorporated in a major aggregate, such as gross domestic product.
10.8 With the release of the June quarter accounts each year another base year is introduced, and because the latest base year is always chosen to be the reference year, the latter is also advanced one year. Rereferencing results in revisions to the levels of the chain volume measures, but it does not result in revisions to growth rates, although growth rates can be revised for other reasons. One reason is that the introduction of a new base year results in revisions to growth rates for the September, December and March quarters of the latest year.
10.9 There are two major reasons for reweighting the quarterly volume measures annually rather than quarterly. First, the prices required to derive quarterly reweighted volume measures for the industry-based measure of GDP are unavailable. Only quarterly reweighted measures of the expenditure-based measure of GDP could be derived. Second, quarterly reweighted measures should only be compiled using seasonally adjusted data, and this would require seasonally adjusting at the most detailed level. The ABS believes that better seasonal adjustments are often obtained by seasonally adjusting at a more aggregate level. Furthermore, some users require quarterly original data. For example, some econometricians much prefer to use original data in their models.
10.10 Benchmarking the quarterly chain volume measures to the annual chain volume measures is done for several reasons. First, it ensures that the quarterly chain volume measures add to the corresponding annual chain volume measures, which are derived from balanced supply and use tables in the prices of the previous year at a more detailed level. Second, in Step 3 above, it was noted that the index for March quarter to June quarter in year t is calculated in year t-1 prices, but that the subsequent index for June quarter to September quarter is calculated in year t prices. It turns out that some aggregates are quite sensitive to when the switch is made from using year t-1 prices to year t prices in the calculation of the quarter-to-quarter indexes. If, for instance, the index from March quarter to June quarter in year t were calculated at year t prices instead of year t-1 prices, then this index could have quite a different value. As a result, year-to-year growth rates of annualised quarterly chain volume measures can vary substantially from those of the corresponding chain volume measures derived directly from annual data. It has been found also that this variation is greatest for those aggregates, such as GDP, which include changes in inventories. In some quarters the difference between changes in inventories valued in the previous year's prices can be substantially different to changes in inventories valued in the current year's prices, while in neighbouring quarters the difference can be quite small or have the opposite sign.
10.11 A method developed by Pierre Cholette of Statistics Canada is used to benchmark the quarterly flow data to the annual data. Let ct and bt denote respectively the unbenchmarked and benchmarked chain volume measures for quarters t. The estimates of bt minimise the sum of (ct /bt - ct-1 /bt-1 )2 over a moving five year span subject to the bts summing to the annual chain volume measure. The values of the bts in the central year are used, except at the ends of the series.
10.12 Series are seasonally adjusted prior to chaining, often at an intermediate level. This presents no problem when using multiplicative seasonal factors, but additive seasonal factors - having been derived from chained or current price data - have to be expressed in the prices of the previous year prior to application. Seasonally adjusted chain volume measures are benchmarked to annual chain volume measures in the same way as the original chain volume measures are benchmarked.
10.13 Although the reference year coincides with the latest base year, the data for the subsequent quarters are not quite additive when generated using the above procedure. This is a consequence of linking on a quarter and using the benchmarking procedure. To ensure additivity over the latest four to seven quarters (i.e. the period from the September quarter following the reference year to the latest quarter), elemental measures from the September quarter following the reference year are added to form the aggregates.
Basic approaches to deriving volume estimates
10.14 As already noted, chain volume estimates are derived by weighting together period-to-period indexes of volume estimates of components at the elemental level, i.e. the lowest level at which volume estimates are derived. Despite their name, the elemental volume estimates are measured in dollars and are in fact usually a bundle of goods and services of a similar type. Most are derived as constant price estimates, but some are chain volume estimates derived indirectly. This section describes the basic approaches taken to derive the elemental volume estimates.
Quantity revaluation
10.15 Two basic approaches can be taken to deriving volume estimates at the elemental level. The first approach uses quantity data to derive constant price estimates: for an individual commodity, the estimate of quantity in each period is multiplied by the price (or average unit value) in some base year. This method, referred to as quantity revaluation, can be applied if the commodity is defined narrowly enough to ensure that it is homogeneous in content and free from quality change over time (since a change in quality is defined as a change in quantum). In some instances data constraints lead to the use of a proxy quantity series which differs from the quantity component of the current price series being revalued. For example, the quantum of services sold by an industry may be assumed to move in the same way as the capacity to provide the service. In other cases, where no appropriate quantity data are available, the constant price value of a commodity may be assumed to move in the same way as the constant price value of a related commodity (or commodities), such as other items of output produced within the same industry.
Price deflation
10.16 The second approach to obtaining volume estimates is referred to as price deflation. A measure of the price component of the current price value is obtained (usually in the form of a price index) and is divided into the current price value in order to revalue it in the prices of the previous year. While the term price deflation suggests that the current price value is being reduced this is not the case when the price index (sometimes called the deflator) in the current period is less than it is in the reference period. In most cases, the price index used is fixed-weighted (i.e. the weights used to combine the constituent price indexes are not changed frequently), but there is one case where the price index is a chain Fisher index (computer equipment) and others where the price index is a chain Paasche price index (gross fixed capital formation for equipment). In those cases where both the price and quantity relativities of the constituents of an elemental component are changing quickly it is important to construct annually reweighted chain price indexes. In those cases where price and quantity relativities are not changing rapidly, reweighting is undertaken less frequently, but usually no less than once every six years.
10.17 Price deflation is the most commonly used method, largely because most macroeconomic statistics are available only as dollar values, and the very detailed quantity data required for quantity revaluation are unavailable. However, there are also advantages in using price deflation in circumstances where it may be possible to employ either approach. Relative price movements are normally more highly correlated between commodities, and between industries, than are relative quantity movements. Therefore, an adequate indicator of price movement can generally be obtained with less data than are required to obtain an equally adequate indicator of quantity movement. There are two other main advantages in using price deflation as opposed to quantity revaluation:
- in compiling price indexes, specific attention can be given more readily to excluding changes that are attributable to quality change, hence ensuring that any quality changes that do occur are automatically reflected as quantum changes; and
- if directly relevant price or quantity data are not available to revalue a current price value, then the proxy price movements of related commodities will usually be more accurate indicators than the proxy quantity movements.
10.18 In compiling its price indexes, the ABS makes a good deal of effort to ensure that as far as practicable they reflect 'pure' price change. When a change in specification of a good or service occurs the ABS does its best to isolate and exclude any change in price attributable to the change in specification. To the extent that this is achieved, the resulting volume estimates reflect improvements (or degradations) in products. For details of how the ABS deals with specification changes in compiling its price indexes refer to The Australian Consumer Price Index: Concepts, Sources and Methods (Cat. no. 6461.0) and Producer and Foreign Trade Price Indexes: Concepts, Sources and Methods (Cat. no. 6419.0).
The compilation of chain volume estimates of GDP
10.19 As described in Chapter 4, there are three approaches to deriving estimates of GDP: the income approach, the expenditure approach and the production approach. It is possible to derive volume measures of GDP using the last two approaches, but it is not possible to derive a volume measure of GDP by summing volume estimates of its income components. The reason is that the income components of GDP either do not have price and quantity dimensions (e.g. gross operating surplus, which is just a residual) or they do not have unique price and quantity dimensions (e.g. wages, for which the price and quantity characteristics differ according to whether they are viewed from the perspective of an employer or of an employee). However, it is possible to derive an income volume measure of GDP by dividing the current price income estimate of GDP by the implicit price deflator (described later in this chapter) of the expenditure estimate of GDP.
10.20 From 1995-96, annual volume estimates of expenditure and production are compiled in the prices of the previous year in an input-output framework. Volume estimates of the supply of commodities by each Australian industry and imports are confronted and balanced with volume estimates of commodities used by Australian industries, final domestic expenditures, changes in inventories and exports. The balance between supply and use for each commodity category ensures that the volume measure of GDP in the prices of the previous year is the same whether it be derived by summing final expenditures and changes in inventories plus exports less imports or by summing the gross value added of each industry and taxes less subsidies on products. In other words the expenditure and production volume estimates of GDP are identical. The estimates in the prices of the previous year are divided by comparable current price estimates for the previous year to derive year-to-year volume indexes. These are chained to form annual chain volume estimates.
10.21 From 1994-95, annual current price estimates of income, expenditure and production are compiled in an input-output framework in parallel with the volume estimates, so that the annual current price and volume estimates of GDP using the income, expenditure and production approaches are identical from 1994-95 for all but the latest year.
10.22 For current price and volume estimates prior to 1994-95, and for quarterly estimates for all years, the estimates using each approach are based on independent sources, and there are usually differences between the I, E and P estimates. Nevertheless, for these periods, a single estimate of GDP is compiled. In chain volume terms, GDP is derived by averaging the chain volume estimates obtained from each of the three independent approaches. The current price estimate of GDP is obtained by reflating the average chain volume estimate by the implicit price deflator derived from the expenditure-based estimates.
10.23 The sources and methods used to derive the various volume estimates are described in the relevant chapters in this manual. Provided below is a summary of the sources and methods used to produce chain volume estimates of GDP using the expenditure and production approaches respectively.
Chain volume estimates of GDP using the expenditure approach
10.24 Quarterly (and annual) chain volume estimates of GDP are compiled by summing volume estimates, expressed in the prices of the previous year, of final expenditures, changes in inventories and exports less imports. The resulting volume estimates of GDP in the prices of the previous year are then chained.
10.25 For most items in household final consumption expenditure, volume estimates are derived by the price deflation method (i.e. dividing current price values in each case by a price index). The available price indexes are, in most cases, fixed-weighted. For some minor items in household final consumption expenditure, where there is a lack of price or quantity data, use is made of implicit price deflators. In the case of computer equipment a chain Fisher price index is used.
10.26 With the remaining components of gross national expenditure, a greater degree of approximation and assumption is involved. In particular, a significant part of capital formation is incurred in relation to unique goods that are not homogeneous over time or for which standard units of quantity cannot be devised. Volume estimation is achieved in such cases by making assumptions about changes in prices which would have occurred had price series existed for the unique goods in question. Thus gross fixed capital formation is revalued using import and producer price indexes for equipment, various building price indexes, road construction price indexes and wage cost and material price indexes for other components of engineering construction. In the case of equipment, a complex model is used to allow the weights of the various import and producer price indexes to vary over time. The model uses data for commodity imports and for commodities manufactured in Australia, and various other sources, to estimate the commodity composition of expenditures on equipment in both the private and public sectors.
10.27 The volume estimation of government final consumption expenditure is based on revaluing inputs - the wages paid, and goods and services purchased - rather than on directly estimating the volume of services provided. This is consistent with the methods used to compile the current price value of final consumption expenditure on goods and services by general government, which is defined as the sum of material costs, labour costs and consumption of fixed capital less any amounts received through charges levied for goods and services provided by general government bodies (see Chapter 14). The volume estimates of wages, and goods and services purchased, are derived using wage cost indexes (compiled as annually - reweighted chain Laspeyres indexes) and material price indexes, and volume estimates of consumption of fixed capital are derived using a perpetual inventory model (described in Chapter 16). Some of the implications for productivity measurement of this method of revaluing government final consumption expenditure are discussed briefly below.
10.28 Import and producer price indexes are used extensively to derive volume estimates of the book values of inventory levels. These are differenced to obtain volume estimates of changes in private non-farm inventories. Farm and public authority inventories are mostly quantity revalued. A number of assumptions are made in the volume estimation of inventories (described in Chapter 17).
10.29 Most exports of goods are quantity revalued. Volume estimates of most of the balance are derived using export price indexes. Volume estimates of exports of services are derived using a range of price indexes, including the consumer price index. The great bulk of the volume estimates of imports of goods and services are obtained by price deflation (using components of the import price index and some price indexes from other countries).
Chain volume estimates of GDP using the production approach
10.30 The gross value added of an industry at current prices is defined to be the difference between the value of output and the value of goods and services (intermediate input) used up in the process of production. In the national accounts, therefore, it is natural to derive volume estimates of gross value added as the difference between volume estimates of output and intermediate input. By mirroring the current price identity, this method ensures the same consistency in the volume accounts as exists in the current price accounts. This is commonly called the double deflation (or net output) method and is used to derive all the annual industry gross value added estimates from 1995-96.
10.31 Double deflation is used in the annual supply and use tables to derive annual estimates of gross value added for each industry in the prices of the previous year. Wherever possible price indexes directly relating to the outputs and inputs are used, but in many cases such price indexes are unavailable. Proxies are often used that are largely based on input prices, i.e. wage cost and material price indexes. Volume estimates of wholesale and retail margins are derived on the assumption that they have the same growth rate as the sales of commodities they relate to.
10.32 With the exception of agriculture, the data required to use double deflation to derive quarterly volume estimates are unavailable, and so an alternative method must be used. For most industries it is assumed that the volume measure of gross value added grows at the same rate as the volume measure of output (the output indicator method). The assumption underlying this method is that in volume terms the ratio of intermediate input to output is stable. In order to ameliorate departures from this assumption as much as possible, quarterly output volume indexes at as detailed a level as practicable are weighted together using the current price estimate of gross value added in the earlier of the two years. The same approach is used for annual data prior to 1995-96.
10.33 For all the goods-producing industries (except agriculture) and nearly all of the private sector dominated service industries volume estimates of output, or proxies for output, are used as quarterly volume indicators of gross value added.
10.34 For service industries, in particular, it is often difficult (if not impossible) to measure the true changes in the quantum of output. In these circumstances, the volume estimation of output is achieved by using the best available proxies. The examples in the following two paragraphs are intended to clarify this point.
10.35 Two basic components are assumed to comprise the output of the transport industry - passenger movement and freight movement. A greater degree of homogeneity is introduced by identifying different kinds of transport - road, rail, air and water transport - and by distinguishing between country and suburban passengers where appropriate, and between a number of different kinds of freight (e.g. mail, livestock, coal or oil). In practice, the measures of quantity used for each mode of transport are passenger-kilometres and tonne-kilometres. However, such measures make no allowance for joint service components such as loading, or for quality changes resulting from variations in speed or frequency of services.
10.36 For the wholesale and retail trade industry, output is assumed to be proportional to the quantum of goods handled. As a result, no allowance is made for changes in the quality of service provided in handling these goods such as more prompt service or extended shopping hours. In the case of the banking industry the principal quarterly output measure is the real value of bank financial assets. Likewise, this measure takes no account of changes in the quality of banking services.
10.37 In the absence of satisfactory alternatives, hours worked data are used as the quarterly indicators of the volume movements in gross value added in the remaining service industries: property and business services; government administration and defence; education; health and community services; much of personal services; and part of cultural and recreational services. The assumption underlying this procedure is that there is no change in volume gross value added per hour worked, i.e. labour productivity is constant.
10.38 In the annual supply and use tables, annual volume measures of the labour income components of the outputs of the general government-dominated industries are derived by deflation, using wage cost indexes. As wages account for the bulk of general government output (defined to be equal to input), this is almost akin to using hours worked as the indicator of change. However, there is one difference worth noting: to the extent that changes in the mix of high and low paid jobs reflect changes in the average skill or productivity level of the workforce, wage-deflated estimates - unlike hours worked based estimates - will reflect productivity growth. It should be noted, though, that such a measure of productivity growth is likely to be only partial.
Price indexes
Introduction
10.39 Just as constant price estimates were replaced by chain volume measures, so the previously published fixed-weighted price indexes have been replaced by chain price indexes. Thus, there are two types of price index published for each of the expenditure aggregates in the national accounts: chain price indexes and implicit price deflators (IPDs) derived from chain volume estimates. One of the benefits of chaining is that, for each aggregate, the growth rates of chain price indexes and IPDs derived from chain volume estimates are generally more alike than the previously published fixed-weighted price indexes and IPDs derived from constant price estimates.
Implicit price deflators
10.40 An implicit price deflator (IPD) is an index obtained by dividing a current price value by its corresponding volume estimate. Thus implicit price deflators are derived measures (hence the term 'implicit') and are not normally the direct measures of price change by which current price estimates are converted to estimates at constant prices. The formula for an IPD derived from annual, annually reweighted chain Laspeyres volume measures in year t is:
10.41 When calculated from the major national accounting aggregates, such as gross national expenditure, IPDs relate to a broader range of goods and services in the economy than that represented by any of the individual consumer and producer price indexes published by the ABS.
10.42 Implicit price deflators provide an estimate of 'pure' price change between a year (the base year) and a period in the following year, and use the quantity weights of this latter period. For quarterly IPDs in the latest year, the pure price change is from the year two years earlier. Because the weights change from period to period, implicit price deflators do not compare the price of a constant basket of goods and services between any two periods except when comparing a period with its base period. Therefore, a change in an IPD between any two periods, neither of which is the base period, represents a combination of the effects of actual price changes between the two periods and the effects of relative changes between those periods in the underlying quantity weights, or physical composition, of the aggregate from which the deflator is derived. It is possible for changes in the physical composition of the relevant aggregate to produce an increase in the IPD between two non-base periods when all component prices have decreased or, conversely, a decrease in the deflator when all component prices have increased. While these may be extreme cases, from time to time significant aberrations do occur in practice, e.g. when a major purchase of a capital good is made by the private sector from the public sector, the IPD for public gross fixed capital formation can be negative.
10.43 IPDs calculated from the quarterly national accounting aggregates may be particularly affected by changes in the physical composition of those aggregates. Much of the quarter-to-quarter change in the physical composition of aggregates is seasonal. Therefore, an IPD derived from seasonally adjusted quarterly data is normally a more reliable indicator of 'pure' price change than one calculated from unadjusted data. However, seasonally adjusting the series may not completely eliminate the impact of seasonal changes on the derived IPDs.
10.44 The limitations outlined in the preceding paragraphs mean that the movement in an individual IPD between two quarters should not be taken as a measure of price change in isolation from other relevant information that is available. For instance, the change in an IPD between two periods should be considered in the context of movements of the IPD around the periods in question. This is particularly important with respect to changes from one quarter to the next.
10.45 Annual movements in IPDs derived from the annually reweighted chain volume estimates are much more reliable indicators of price change than the quarterly movements, because they do not suffer from the effects of compositional change and are measures of pure price change. However, if quarterly measures of pure price change are required it is better to use the chain price indexes (see paragraphs 10.47 to 10.49).
10.46 IPDs are subject to revision because of revisions in the relevant current price and/or chain volume estimates, including changes to seasonally adjusted estimates resulting from seasonal reanalysis. In particular, quarterly estimates as first published are sometimes revised substantially when firmer data become available.
Chain price indexes
10.47 The chain price indexes published in the national accounts are annually reweighted chain Laspeyres price indexes and are analogous to chain volume estimates. They comprise the deflators used to derive the volume estimates, weighted together in the same way and at the same level of detail as the chain volume estimates. In those cases where quantity revaluation is used to derive volume estimates the IPD is used in constructing the chain price indexes. However, these IPDs are calculated at such a detailed level that for all intents the published national accounts chain price indexes can be considered as measures of pure price change.
10.48 Chain price indexes are not the only price indexes published by the ABS that measure pure price change. The consumer price index and all the producer and international trade price indexes also do this. However, the chain price indexes have some useful features that these other price indexes do not share at present. First, they encompass the whole of the economy, and second, they are frequently reweighted.
10.49 The detailed price components of the chain price indexes are drawn from ABS producer, international trade, wage cost and consumer price indexes, as well as various sources outside the ABS. This reflects the fact that national accounts aggregates and their associated chain price indexes have a broader scope than related ABS fixed-weighted price indexes, and for some items they adopt different conceptual treatments. As a result of these differences and the fact that they are chained, the chain price indexes differ from related fixed-weighted price indexes published by the ABS. A more detailed comparison of the fixed-weighted equivalents of the Consumer Price Index (CPI), Import Price Index (IPI) and Export Price Index (EPI) is given below.
The chain price index for household final consumption expenditure (HFCE) compared with the CPI
10.50 Movements in the chain price index for HFCE are generally very close to movements in the CPI due to the fact that most parts of HFCE are deflated by components of the CPI. However, differences do occur between the two price indexes in some quarters. Some of the more important reasons for these differences are:
- The CPI is reweighted every four or five years, whereas the chain price index is reweighted every year.
- The chain price index uses a range of price indexes, apart from CPI component series, including producer price indexes, wage cost indexes, stock exchange indexes, and public sector deflators relating to education and hospital expenditure.
- HFCE is broader in scope and relates to expenditure by all Australian resident households and private non-profit institutions serving households whereas the CPI relates to expenditure carried out in Australian resident households of the eight capital cities of the States and Territories.
- The national accounts concept and treatment of HFCE differs from household consumer expenditure as measured by the CPI. Some of the more significant differences are mentioned below, while further details can be found in Chapter 14, and in The Australian Consumer Price Index: Concepts, Sources and Methods (Cat. no. 6461.0).
- HFCE excludes expenditure by persons on the purchase and maintenance of dwellings, but imputes rental payments for owner-occupied dwellings. The CPI represents home ownership costs by actual rents, net house purchase (new dwellings excluding land plus alterations and additions), property rates and charges, house repairs and maintenance and house insurance.
- Included in HFCE are several items not covered by the CPI. Major goods and services affected are expenditure on gambling and a range of financial services, such as bank charges (both direct and indirect), the administrative costs of life insurance offices and superannuation funds, and share brokering commissions.
- Expenditure on food and drinks in cafes, restaurants and clubs is included in the HFCE category Hotels, cafes and restaurants, while these expenditures are included in Food in the CPI.
10.51 The conceptual and coverage differences mentioned above, together with the different base periods of the chain price index and the CPI, result in different weights being used in each index when measuring similar components. Some examples are given below in respect of the June quarter 1998:
 |
|  |
 | Item | CPI weight (per cent)
(as per the 13th series of the CPI) | Chain price index weight (per cent) |  |
 |
|  |
 | Food | 19.2 | 12.2 |  |
 | Private motoring | 13.2 | 10.0 |  |
 | Rent | 5.8 | 17.9 |  |
 | Cigarettes and tobacco | 3.1 | 1.9 |  |
 | Alcoholic drinks | 5.1 | 1.2 |  |
 | Health | 3.8 | 3.8 |  |
 | Recreation and culture | 5.8 | 11.6 |  |
 |
|  |
The chain price index for exports and imports of goods and services compared with the EPI and IPI
10.52 Both the EPI and the IPI published by the ABS have displayed different price movements from their counterpart national accounts chain price indexes over time. The major reasons for these differences are as follows:
- The EPI and IPI were reweighted relatively infrequently (at 5 yearly or longer intervals until the September quarter 2000, when they became annually reweighted and chained), whereas the chain price index is reweighted annually from 1985-86.
- The chain price indexes in the national accounts cover goods and services, while both the EPI and IPI only cover goods.
- Both chain price indexes are formed by weighting price indexes for services and component IPDs for goods. The goods IPDs are derived at the division level of the Standard International Trade Classification (SITC) and comprise 109 import categories and 66 export categories. The IPDs at the division level for exports are derived from volume estimates formed by quantity revaluing a significant proportion of exports and then deflating the remainder at the division level using appropriate price indexes. The use of IPDs in the construction of the chain price indexes is a weakness, but it is substantially ameliorated by the detailed level at which they are weighted together.
|
 Print Page
Print Page
 Print All
Print All