TECHNICAL NOTE SAMPLING AND NON-SAMPLING ERROR
RELIABILITY OF ESTIMATES
1 As the estimates in this publication are based on information relating to a sample of employers and employees, rather than a full enumeration, they are subject to sampling variability, that is, they may differ from the figures that would have been produced if the data had been obtained from all employers and all employees. The difference, called sampling error, should not be confused with inaccuracy that may occur because of imperfections in reporting by respondents or in processing by the ABS. Such inaccuracy is referred to as non-sampling error and may occur in any enumeration whether it be a full count or a sample. Efforts have been made to reduce non-sampling error by careful design of questionnaires, detailed checking of returns and quality control of processing.
2 The sampling error associated with any estimate can be estimated from the sample results. One measure of sampling error is given by the standard error, which indicates the degree to which an estimate may vary from the value that would have been obtained from a full enumeration (the ‘true value'). There are about two chances in three that a sample estimate differs from the true value by less than one standard error, and about nineteen chances in twenty that the difference will be less than two standard errors. Standard errors are available in the electronic data release accompanying this publication (see data cube 10).
3 An example of the use of a standard error is as follows. From the publication, the estimated average weekly total cash earnings for all employees paid by collective agreement is $1,150.80, with a standard error of $13.20 (from the standard error data cube). There would be about two chances in three that a full enumeration would have given an estimate in the range $1,137.60 to $1,164.00 and about nineteen chances in twenty that it would be in the range $1,124.40 to $1,177.20.
4 The difference between two survey estimates is also an estimate and it is therefore subject to sampling variability. The standard error on the difference between two survey estimates in the one time period (i.e. x-y) can be calculated using the following formula:
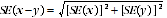
5 The formula above will overestimate the standard error where there is a positive correlation between two estimates (e.g. male and female school teachers). While this formula will only be accurate where there is no correlation between two estimates (e.g. estimates from different states), it is expected to provide a reasonable approximation of the standard error for the difference between two survey estimates.
6 From the publication, the estimated average weekly total cash earnings for all male employees is $1,342.50, with a standard error of $15.10 (from the standard error data cube). For all female employees the estimated average weekly total cash earnings is $904.00 with a standard error of $8.70. Thus the difference between the estimate of male and female earnings is $438.50. The estimate of the standard error of the difference between the average weekly total cash earnings employees of males and females is:
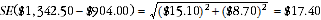
7 There are about two chances in three that the true figure for the difference between average weekly total cash earnings for males and females lies in the range $421.10 to $455.90, and about nineteen chances in twenty that the figure is in the range $403.70 to $473.30.
8 The formula above can be used to estimate the standard error on a difference between estimated averages in two different years. (The movement standard error will be approximately 1.4 times the standard error on the level estimate, if the standard errors on the two level estimates are similar.)
9 Another measure of the sampling error is the relative standard error, which is obtained by expressing the standard error as a percentage of the estimate.
10 An asterisk appears against an estimate in this publication where the sampling variability is considered high. For the tables in this publication, estimates with relative standard errors above 25% have been labelled with a cell comment.
11 Standard errors can be used to construct confidence intervals around the estimated proportions. There are about two chances in three that the 'true' value is within the interval that ranges from the sample estimate minus one standard error (estimate - 1xSE) to the sample estimate plus one standard error (estimate + 1xSE). There are approximately 19 chances in 20 that the 'true' value lies within the interval from the estimate minus two standard errors (estimate - 2xSE) to the estimate plus two standard errors (estimate + 2xSE).
12 The above rule gives a symmetric confidence interval that is reasonably accurate when the estimated proportion is not too near 0.00 or 1.00. Where the estimated proportion is close to 0.00 or 1.00 it would be more accurate to use a confidence interval that was not symmetric around the sample estimate. If an estimate is close to 1.00, then the upper boundary of the confidence interval should be closer to the sample estimate than suggested above, while the lower boundary should be further from the sample estimate. Similarly, if an estimate is close to 0.00, then the lower boundary of the confidence interval should be closer to the sample estimate than suggested above, while the upper boundary should be further from the sample estimate. In particular, the symmetric confidence interval could include values that are not between 0.00 and 1.00. In such a case a good rule of thumb is to use a confidence interval of the same size as the symmetric one, but with the lower (or upper) boundary set to 0.00 (or 1.00).
13 Data cube 10 contains estimates of standard errors from which confidence intervals may be constructed.
 Print Page
Print Page
 Print All
Print All
 Quality Declaration
Quality Declaration