TECHNICAL NOTE DATA QUALITY
RELIABILITY OF THE ESTIMATES
1 Since the estimates in this publication are based on information obtained from occupants of a sample of dwellings, they are subject to sampling variability. That is, they may differ from those estimates that would have been produced if all dwellings had been included in the survey. One measure of the likely difference is given by the standard error (SE), which indicates the extent to which an estimate may have varied by chance because only a sample of dwellings was included. There are about two chances in three (67%) that a sample estimate will differ by less than one SE from the number that would have been obtained if all dwellings had been included, and about 19 chances in 20 (95%) that the difference will be less than two SEs.
2 Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate.
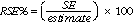
3 RSEs for estimates from 2010 SEW were calculated for each separate estimate and published in the 'direct' form. The Jackknife method of variance estimation is used for this process, which involves the calculation of 30 'replicate' estimates based on 30 different sub samples of the original sample. The variability of estimates obtained from these sub samples is used to estimate the sample variability surrounding the main estimate.
4 Tables 2, 7, 8, 21 and 22 contain estimates collected from previous Education and Work surveys. The spreadsheets associated with this release contain RSEs for these estimates. The RSEs for the years 2001 and 2003 were calculated using the previous statistical SE models, which are available from each relevant issue of Education and Work, Australia (cat. no. 6227.0) available on the ABS website <www.abs.gov.au>. For the 2005, 2007 and 2008 data, the RSEs were directly calculated for each separate estimate. This method differs from that presented in the 2005 publication, which describes using statistical SE models to calculate RSEs for all time points. While the direct method is more accurate, the difference between the two is usually not significant for most estimates.
5 In the tables in this publication, only estimates (numbers, percentages, means and medians) with RSEs less than 25% are considered sufficiently reliable for most purposes. However, estimates with larger RSEs are included and preceded by an asterisk (e.g. *1.3) to indicate they are subject to high SEs and should be used with caution. Estimates with RSEs greater than 50% are preceded by a double asterisk (e.g. **0.6) to indicate that they are considered too unreliable for general use.
CALCULATION OF STANDARD ERROR
6 Standard errors can be calculated using the estimates (counts or means) and the corresponding RSEs. For example, Table 1 shows the estimated number of females in Victoria enrolled in a course of study was 386,500. The RSE Table corresponding to the estimates in Table 1 (see Table 1 Relative Standard Errors in the 'Relative Standard Error' section at the end of these Technical Notes) shows the RSE for this estimate is 3.0%. The SE is calculated by:

7 Therefore, there are about two chances in three that the value that would have been produced if all dwellings had been included in the survey will fall within the range 374,900 to 398,100 and about 19 chances in 20 that the value will fall within the range 363,300 to 409,700. This example is illustrated in the diagram below:

Proportions and percentages formed from the ratio of two estimates are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. A formula to approximate the RSE of a proportion is given below. This formula is only valid when x is a subset of y.
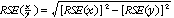 9
9 As an example, using estimates from Table 1, of the 741,500 persons enrolled in a course of study in Victoria, 355,000 are males, or 47.9%. The RSE for 355,000 is 3.4% and the RSE for 741,500 is 2.3% (see Table 1 Relative Standard Errors in the section 'Relatice Standard Error' at the end of these Technical Notes). Applying the above formula, the RSE for the proportion of males in Victoria enrolled in a course of study:
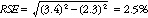 10
10 Therefore, the SE for the proportion of males in Victoria enrolled in a course of study is 1.2 percentage points (=(2.5/100) x 47.9). Hence, there are about two chances in three that the proportion of males in Victoria enrolled in a course of study is between 46.7% and 49.1%, and 19 chances in 20 that the proportion is between 45.5% and 50.3%.
DIFFERENCES
11 Published estimates may also be used to calculate the difference between two survey estimates (of numbers or percentages). Such an estimate is subject to sampling error. The sampling error of the difference between two estimates depends on their SEs and the relationship (correlation) between them. An approximate SE of the difference between two estimates (x-y) may be calculated by the following formula:
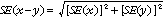 12
12 While this formula will only be exact for differences between separate and uncorrelated characteristics or sub populations, it is expected to provide a good approximation for all differences likely to be of interest in this publication.
SIGNIFICANCE TESTING
13 A statistical significance test for any of the comparisons between estimates can be performed to determine whether it is likely that there is a difference between the corresponding population characteristics. The standard error of the difference between two corresponding estimates (x and y) can be calculated using the formula in paragraph 12. This standard error is then used to calculate the following test statistic:
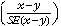 14
14 If the value of this test statistic is greater than 1.96 then there is statistical evidence of a significant difference in the two populations with respect to that characteristic. This statistic corresponds to a 95% confidence interval of the estimate. Otherwise, it cannot be stated with confidence that there is a real difference between the populations.
15 The imprecision due to sampling variability, which is measured by the SE, should not be confused with inaccuracies that may occur because of imperfections in reporting by respondents and recording by interviewers, and errors made in coding and processing data. Inaccuracies of this kind are referred to as non-sampling error, and they occur in any enumeration, whether it be a full count or sample. Every effort is made to reduce non-sampling error to a minimum by careful design of questionnaires, intensive training and supervision of interviewers, and efficient operating procedures.
RELATIVE STANDARD ERROR
16 Limited publication space does not allow for the separate indication of the SEs and/or RSEs of all the estimates in this publication, only RSEs for Table 1 are included below. However, RSEs for all tables are available free-of-charge on the ABS website
<www.abs.gov.au>, released in spreadsheet format as an attachment to this publication,
Education and Work, Australia, May 2009 (cat. no. 6227.0).
TABLE 1 RELATIVE STANDARD ERRORS, Persons aged 15-64 years enrolled in formal or non-formal learning - Selected characteristics-by state or territory of usual residence |
|
 |  |  |  | NSW | Vic. | Qld | SA | WA | Tas. | NT | ACT | Aust. |
 |  |  |  | % | % | % | % | % | % | % | % | % |
|
| Sex |  |  |  |  |  |  |  |  |  |
 | Males | 2.8 | 3.4 | 3.2 | 4.7 | 5.1 | 3.9 | 7.8 | 6.7 | 1.9 |
 | Females | 2.4 | 3.0 | 2.8 | 4.1 | 4.0 | 5.2 | 7.8 | 4.9 | 1.8 |
| Age group (years) |  |  |  |  |  |  |  |  |  |
 | 15-19 | 2.1 | 2.1 | 2.7 | 3.3 | 3.8 | 3.0 | 8.3 | 2.4 | 1.1 |
 | 20-24 | 4.0 | 4.4 | 4.7 | 5.2 | 8.5 | 9.8 | 15.1 | 7.7 | 2.2 |
 | 25-34 | 6.5 | 5.5 | 5.7 | 8.3 | 12.1 | 9.4 | 14.2 | 10.8 | 4.1 |
 | 35-44 | 6.8 | 10.4 | 8.7 | 12.5 | 9.4 | 10.6 | 13.0 | 9.9 | 3.8 |
 | 45-54 | 9.4 | 12.0 | 10.8 | 13.8 | 12.9 | 13.4 | 17.3 | 19.1 | 4.9 |
 | 55-64 | 15.5 | 17.9 | 16.4 | 18.8 | 23.8 | 24.3 | 40.7 | 29.2 | 7.7 |
| Country of birth |  |  |  |  |  |  |  |  |  |
 | Born in Australia | 2.5 | 3.5 | 2.6 | 3.9 | 3.5 | 3.1 | 7.5 | 4.1 | 1.6 |
 | Born overseas | 4.9 | 7.7 | 8.2 | 10.0 | 8.3 | 19.7 | 14.2 | 15.8 | 3.3 |
| Area of usual residence |  |  |  |  |  |  |  |  |  |
 | State capital city | 2.4 | 2.4 | 3.5 | 3.2 | 3.4 | 5.6 | - | - | 1.7 |
 | Balance of state/Territory | 3.6 | 4.6 | 3.8 | 10.1 | 9.3 | 5.5 | 6.4 | 4.0 | 2.0 |
| Labour force status |  |  |  |  |  |  |  |  |  |
 | In labour force | 3.1 | 3.4 | 2.8 | 5.3 | 5.3 | 4.9 | 7.0 | 5.0 | 1.8 |
 |  | Employed | 3.3 | 3.4 | 3.2 | 5.0 | 5.5 | 5.4 | 6.6 | 5.5 | 1.9 |
 |  |  | Employed full time | 3.9 | 5.4 | 4.4 | 11.3 | 6.4 | 9.4 | 9.6 | 8.8 | 2.4 |
 |  |  | Employed part time | 4.9 | 3.3 | 5.1 | 5.5 | 8.4 | 8.5 | 9.9 | 6.5 | 2.3 |
 |  | Unemployed | 9.4 | 12.0 | 14.2 | 18.3 | 26.6 | 23.2 | 74.4 | 23.1 | 6.0 |
 | Not in labour force | 3.6 | 4.1 | 4.9 | 5.2 | 5.6 | 6.8 | 13.0 | 11.0 | 2.4 |
| Level of formal or non-formal learning in May 2010(a) |  |  |  |  |  |  |  |  |  |
 | Formal learning(b) | 2.1 | 2.4 | 2.7 | 3.5 | 3.7 | 2.9 | 7.0 | 4.0 | 1.5 |
 |  | Postgraduate Degree | 10.5 | 9.1 | 13.6 | 14.8 | 24.2 | 18.7 | 31.3 | 17.6 | 6.4 |
 |  | Graduate Diploma/Graduate Certificate | 18.2 | 15.3 | 24.4 | 23.4 | 28.8 | 31.1 | 48.8 | 20.4 | 9.2 |
 |  | Bachelor Degree | 5.9 | 5.3 | 6.7 | 5.3 | 8.1 | 11.3 | 18.6 | 11.2 | 3.0 |
 |  | Advanced Diploma/Diploma | 8.3 | 8.2 | 10.5 | 14.1 | 10.4 | 21.9 | 21.8 | 19.2 | 3.9 |
 |  | Certificate III/IV | 7.3 | 7.1 | 6.9 | 11.8 | 12.1 | 12.4 | 11.2 | 15.8 | 4.1 |
 |  | Certificate I/II | 14.4 | 19.2 | 22.6 | 23.4 | 25.4 | 31.9 | 51.1 | 56.3 | 10.1 |
 |  | Certificate n.f.d. | 12.4 | 16.4 | 22.2 | 22.7 | 19.9 | 35.3 | 30.3 | 35.5 | 6.0 |
 |  | Year 12 or below | 2.2 | 2.6 | 3.3 | 3.3 | 4.5 | 4.4 | 7.2 | 3.9 | 1.3 |
 | Non-formal learning | 10.6 | 9.9 | 18.3 | 21.3 | 18.1 | 25.6 | 32.9 | 27.3 | 6.3 |
| Type of educational institution |  |  |  |  |  |  |  |  |  |
 | Secondary education | 2.2 | 2.6 | 3.0 | 3.4 | 4.4 | 4.7 | 7.2 | 4.1 | 1.3 |
 | TAFE | 4.9 | 6.3 | 4.7 | 9.9 | 7.8 | 10.5 | 19.0 | 14.5 | 2.7 |
 | Higher education | 5.4 | 4.0 | 6.2 | 4.5 | 8.5 | 7.7 | 9.8 | 7.5 | 3.0 |
 | Other institution | 6.8 | 7.7 | 5.8 | 10.2 | 11.1 | 11.0 | 16.4 | 18.7 | 3.7 |
| Type of enrolment |  |  |  |  |  |  |  |  |  |
 | Full-time enrolment | 2.6 | 2.6 | 3.6 | 3.3 | 4.4 | 4.4 | 10.6 | 5.2 | 1.6 |
 | Part-time enrolment | 3.5 | 4.6 | 3.9 | 8.0 | 6.3 | 7.4 | 6.7 | 8.3 | 2.0 |
| Total | 1.9 | 2.3 | 2.3 | 3.6 | 3.6 | 2.7 | 6.4 | 4.0 | 1.4 |
|
| - nil or rounded to zero (including null cells) |
| (a) The levels of formal and non-formal learning are not necessarily listed in order from highest to lowest. For further details see paragraphs 19-21 of the Explanatory Notes. |
| (b) Includes 'Level not determined'. |
 Print Page
Print Page
 Print All
Print All
 Quality Declaration
Quality Declaration