Contents >>
Chapter 6. Compiling the Indexes of the LPI
INTRODUCTION
6.1 The LPI provides a measure of changes in the price of labour services purchased by employers across the various segments of the labour market and between two or more time periods.
6.2 This chapter provides details on how the various indexes of the LPI are constructed. The first step in the process, collecting price data, has already been covered in previous sections. Therefore, the starting point for this chapter is that weighted average prices for elementary aggregates have been calculated. The chapter provides information on the calculation of price relatives and how these are combined with expenditure weights to construct index numbers. It concludes with information on the construction of the labour price index.
PRICE RELATIVES FOR ELEMENTARY AGGREGATES
6.3 When calculating the LPI, a Laspeyres-type price index, prices are compared between the current period and the base period. The process involves calculating the current to base period price relative Pt / PB where Pt is the price in the current period and PB is the price in the base period. A price relative (Pt / PB) is calculated for each segment of the labour market (elementary aggregate) which compares the weighted average EA price in the current period with the weighted average EA price in the base period.
6.4 Price relatives are calculated at the EA level for each of the wage and non-wage price indexes.
6.5 Tables 6.1 below demonstrates the calculation of price relatives for total hourly rates of pay for three elementary aggregates.
Table 6.1: Calculation of Price Relatives |
|  |
 | Weighted Average Prices
| Price Relatives (R)
|  |
| Elementary Aggregates | P0 | P1 | P2 | R1 | R2 |  |
|  |
| 1 | 13.65 | 14.36 | 15.12 | 1.0520 | 1.1077 |  |
| 2 | 12.89 | 15.54 | 15.63 | 1.2056 | 1.2126 |  |
| 3 | 11.45 | 11.62 | 12.98 | 1.0148 | 1.1336 |  |
|  |
6.6 It is possible that a price relative might not be able to be calculated for all EAs. Although rare, this can arise when there are no matched jobs in an EA. In this situation a price relative is estimated using the price relatives of other closely related EAs.
EXPENDITURE WEIGHTS
6.7 The LPI provides a measure of the average rate of price change across all labour services purchased by employers in Australia. In calculating an average of price changes across these labour services it needs to be recognised that some employers are significantly larger than others and so are more important in terms of their share of overall employer expenditure. The aggregate indexes need to be compiled by weighting price movements relative to their importance in the overall expenditure levels of employers.
6.8 As outlined in 3.14, the indexes of the LPI are compiled using an alternative method of calculating a Laspeyres price index. Under this approach price relatives between the current period and the base are weighted by their shares of labour expenditure in the base period.
6.9 The calculation of these expenditure shares for LPI are discussed in more detail in Chapter 3.
Annual reweight
6.10 To ensure the index remains relevant, the expenditure shares need to be regularly updated to reflect changes in the expenditure patterns of employers. Once updated, the weights are fixed again, and a new weighting base is created. In the following periods, prices will be compared using this new weighting base. The LPI has been reweighted annually since its inception.
6.11 When the expenditure weights are updated, it does not follow that the published index numbers will recommence at 100.0, as the reference base (as opposed to the weighting base) which is currently the financial year 2003-04, may not be updated. Instead, the series based on the old expenditure weights and that based on the new expenditure weights are linked to form a continuous series via an arithmetic calculation, in a process referred to as chaining (see paragraph 2.16 to 2.18).
INDEX NUMBERS
6.12 In the LPI, index numbers are created by combining price relatives using expenditure shares. This is represented by the following formula
(6.1)
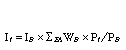
where the summation is across all EAs,
It is the index value for the current period
IB is the index value for the base period
WB is the base period expenditure share for each EA
Pt is the current period weighted average price for each EA
PB is the base period weighted average price for each EA.
6.13 Each index (e.g. Australia, states/territories, sector etc.) represents the amalgamation of a number of EA price relatives. All of the various wage and non-wage price indexes are calculated in this manner. Obviously, the combination of EAs and their expenditure shares varies depending on the index being compiled.
6.14 The table below demonstrates the index calculation process. If we assume that the NSW, private sector is split into 3 EAs (EA1, 2 and 3), the table outlines the calculation of the total hourly rates of pay index for the NSW private sector.
Table 6.2: Aggregation of Elementary Aggregates to form an Index |
|  |
 |  | Price relative
| Index
|  |
| Elementary Aggregate | Expenditure Weight | RB | R1 | R2 | IB | I1 | I2 |  |
|  |
| 1 | 36,000 | 1.0000 | 1.0520 | 1.1077 | - | - | - |  |
| 2 | 25,000 | 1.0000 | 1.2056 | 1.2126 | - | - | - |  |
| 3 | 21,000 | 1.0000 | 1.0148 | 1.1336 | - | - | - |  |
| Index |  |  |  |  | 100.0 | 108.9 | 114.6 |  |
|  |
6.15 As noted above, indexes can be calculated for various combinations of state/territory, sector, industry and occupation. However, occupation indexes are only available for wage price indexes. The specific outputs available are discussed further in chapter 7.
CONSTRUCTION OF THE LABOUR PRICE INDEX
6.16 The labour price index is constructed from the individual wage and non-wage components. Two versions of the labour price index are produced, differentiated by the exclusion or inclusion of bonuses. Only those indexes that exclude bonuses are pure price indexes. Bonus payments can reflect changes in the quality of work performed (see paragraph 4.40).
6.17 The same formula as that above is used to calculate the labour price indexes. However, rather than weighting together the EA price relatives for one specific wage or non-wage component, the EA price relatives for the total hourly rates of pay (either excluding or including bonuses) are combined with the EA price relatives for all of the non-wage components.
 Print Page
Print Page
 Print All
Print All