FEATURE ARTICLE: MEASURING CHANGES IN LABOUR COSTS
INTRODUCTION
Labour costs are the costs incurred by employers in the employment of labour. These costs include wages and salaries, paid leave, superannuation, taxes on employment, training and recruitment costs, and fringe benefits (included in wages and salaries in the national accounts). They are of particular interest as they impact on the competitiveness of organisations and employers willingness to employ. They also form the predominant component of household income, and as such have a significant impact on household consumption, investment and saving decisions.
Understanding movements in wages and labour costs is important in assisting the formulation of macro-economic policy and in making wage determinations for individual businesses. When examining labour costs, decision makers do not usually consider nominal wages in isolation. They consider real wages, that is, wages adjusted for the effect of prices, and they also take into account changes in labour productivity and its subsequent effect on labour costs.
The ABS produces a range of statistics relating to employee remuneration and the price of labour. These statistics have been developed to meet the needs of users for information on the returns to labour from economic production, the level of employee earnings, and labour costs and prices. Relevant series include the compensation of employees from the Australian National Accounts, average weekly earnings and the labour price index.
Another labour cost measure not currently compiled by the ABS but which takes into account labour productivity is called a unit labour cost (ULC) measure. A ULC represents a link between productivity and the cost of labour in producing output.
This feature article examines the definitions of various labour cost measures and the links between them, highlighting issues of interpretation. The article also discusses some of the associated measurement issues and presents a graphical comparison of the various alternatives. It also discusses the link between wages and productivity and defines measures of ULC and real unit labour costs (RUCL).
WHY MEASURE LABOUR COSTS?
There are a number of labour cost measures that the ABS produces, and these different measures reflect different concepts. Measures of average weekly earnings and compensation of employees per employee measures are designed to measure the average level of wages or labour costs per employee, while the labour price index measures price changes for a basket of constant quality jobs. Each of these measures is examined further in the following section.
While these measures are useful for understanding developments in the labour market, they do not provide a more direct understanding of how growth in labour costs relates to growth in output or changes in inflation. In this regard a more ideal measure of labour costs should provide an indication of the excess labour cost growth that may create cost or inflationary pressures. Such a measure would take into account productivity improvements that would alleviate cost pressures faced by firms and may also take into account relative price growth between labour costs and general inflation.
Real and nominal measures of unit labour costs (ULC) provide this type of information. A nominal ULC measures the average cost of labour per unit of output while a real ULC adjusts for general inflation. Positive growth in a real ULC indicates that cost pressures exist.
For all labour cost measures there are important uses for the data in measuring changes over time but there are also requirements to measure relativities (e.g. across industries) in labour costs at points in time.
CURRENT ABS LABOUR COST MEASURES
Labour price index (LPI)
The wage, non-wage and labour price indexes contained in the Labour Price Index, Australia (cat. no. 6345.0) measure changes over time in the price of labour unaffected by changes in the quality or quantity of work performed. A range of procedures have been developed to identify and measure quality and quantity changes and ensure that only pure price changes are reflected in the indexes. The specific quality adjustments performed (ABS 2006) are changes in:
- the nature of work performed (for example, different tasks or responsibilities)
- the quantity of work performed (for example, the number of hours worked)
- the characteristics of the job occupant (for example, age, apprenticeship year, successful completion of training or a qualification, grade or level, experience, etc.)
- other price determining characteristics which may exist (for example, the site where the work is performed, the presence of other components of pay or labour costs which have been rolled in, changes in work schedules, etc.).
The LPI is an input price index (or purchase price) covering wage and non-wage costs designed to measure changes over time in the cost to businesses of purchasing a fixed quantity and quality of labour input, irrespective of the output produced. Consequently, when considering price movements for jobs, no adjustment is made for productivity changes within the production process that arise from factors such as capital investment, technological change, more efficient organisational arrangements, and entrepreneurial activities.
The wage and salary component of the LPI is the Wage Price Index (WPI). Wages and salaries account for the majority of expenditure on labour costs, around 87% in 2002-03. These wage costs are similar in concept to the wages and salary component of compensation of employees (COE) as measured in the national accounts, and do not include payroll tax or any other taxes payable by the employer on the wage and salary bill.
The LPI and the WPI are unaffected by changes in the composition of the workforce from one quarter to the next as only jobs that have a price for consecutive quarters are considered. The LPI measures the change in the price of labour services resulting from labour market demand pressures. However, changes in the composition of the workforce over time are reflected in the index weights.
Average weekly earnings (AWE)
The purpose of the AWE survey is to measure average gross weekly earnings associated with employee jobs in Australia. The results are published quarterly in Average Weekly Earnings, Australia (cat. no. 6302.0). The AWE is derived by dividing estimates of gross weekly earnings by estimates of number of employee jobs. The AWE does not relate to average award rates of pay or to the earnings of the 'average employee' (ABS 2006).
The AWE measure is a wage bill indicator whereas the LPI includes both wage and non-wage costs. Hence, it is more appropriate to compare the AWE to the WPI. Changes in AWE may be affected by changes in weekly hours worked (or paid for) and by changes in the composition of jobs in the workforce. These compositional effects in the AWE highlight the main difference between AWE and the WPI, as the methodology implemented in the WPI means it is unaffected by compositional change.
Compositional changes can be the result of variation in the proportions of full-time, part-time, casual, adult and junior employment, and variations in the proportions of males and females employed. Changes in the distribution of employees between industries and variations in the occupational distribution within and across industries may also affect measures. For example, assuming hourly rates of pay remain constant, but individuals are shifting into higher paid jobs then labour costs, as measured by the AWE, will increase, while the LPI would remain unchanged. Another example, where labour costs increase but the LPI would be unchanged is a shift from part-time to full-time work. In this example, growth in AWE would increase as employees are working longer hours and are paid for these extra hours, even though their pay rates remain unchanged.
Compensation of employees (COE)
COE is a National Accounts measure that includes the value of entitlements earned by employees from their employers for services rendered during the accounting period. COE is further classified into two sub-components: wages and salaries, and employers' social contributions. COE excludes indirect taxes payable by the employer on the wage and salary bill, for example, payroll tax, although COE does include fringe benefits tax. COE provides a wider measure than employee earnings as it includes severance and termination payments, all irregular remuneration such as irregular bonuses, ad hoc bonuses and exceptional payments. It also includes all wages and salaries in kind in the form of consumption goods and services produced or purchased by the employer and provided free of charge or offered to employees at reduced prices, including welfare services (ABS, 2006).
Compositional changes in the workforce affect average COE per employee in the same way as AWE. Therefore, circumstances such as increases in the proportion of higher paid or full-time jobs will increase average COE and AWE holding all other influences constant. The main two differences between COE and AWE are the inclusion of non-wage labour costs in COE and differences in source data.
The change in COE per employee, that is average COE, is not equal to the change in the LPI or the WPI, as average COE will change as the composition of jobs or hours worked changes whilst the LPI and WPI will remain unchanged. Neither average COE nor AWE takes into account the affect productivity improvements have on labour costs.
THE LINK BETWEEN WAGES AND PRODUCTIVITY
In general, productivity growth leads to growth in average output and hence growth in business income (Parham et al 2000). Any increase in income is distributed by payments to the factors of production, labour (wages) and capital (operating surplus). In addition, consumers might benefit from the distribution of productivity improvements through lower prices.
Within this broad context this article examines the links between wages, labour productivity and changes in the cost of labour. The article does not look at the distributional impacts of any increases in income between capital and labour. Further, it does not examine the distribution of any increase in labour income across wage levels, occupations or industry.
An important assumption that is necessary for analysing the link between wages and productivity is that of perfect competition, which implies that the marginal products of the factors of production are paid their market clearing rate. Thus, for labour, the assumption is that the real wage equals the marginal product of labour. This is also an essential assumption of the multifactor productivity (MFP) framework.
The link between wages and productivity can be shown using a production function, represented by the following equation:
(1) 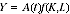
Where
Y = output
K = capital input
L = labour input
A = multifactor productivity.
From equation 1, growth in output comes about from either growth in inputs (capital, labour, or both) or growth in MFP. Further, a proportional relationship between productivity and wages comes from the elasticity of output with respect to labour, as shown in equation 2:
(2) 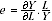
Where
e = the elasticity of output with respect to labour.
Rearranging 2 gives
(3) 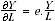
In a perfectly competitive framework where factors are paid their marginal products, the elasticity of output with respect to labour can be equated to the labour income share. Hence, using the assumption that the real wage is equal to the marginal product of labour, equation 3 then becomes:
(4) 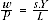
Where
w = nominal wage
p = general price deflator
Y/L = labour productivity
s = labour income share.
Equation 4 shows the real wage (w/p) is equal to the labour income share (s) multiplied by labour productivity. That is, the real wage is proportional to labour productivity.
UNIT LABOUR COSTS (ULC)
ULC are an indicator of the average cost of labour per unit of output produced in the economy. This implies that unit labour costs are costs associated with the employment of labour adjusted for labour productivity. As a result, if there is an increase in average labour costs and there is a commensurate increase in labour productivity there will be no change in the unit labour cost. In contrast to the ULC, the increase in labour costs associated with increased productivity would be reflected in an increase in the LPI, average COE and AWE.
Broadly, unit labour costs are defined as:
(5) 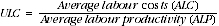
Average labour costs (ALC) are generally calculated as compensation of employees plus payroll tax minus employment subsidies divided by total hours worked by employees. Training and recruitment costs are excluded due to measurement difficulties.
Average labour productivity (ALP) is commonly defined as real gross value added (the volume of output minus the volume of intermediate consumption) divided by the number of total hours worked. Total hours worked here includes not only hours worked by employees, but also by employers and the self-employed. This is because it is not possible to decompose real gross value added into an 'employee only' component. As labour productivity includes employees, employers and the self-employed, changes in it can come from both the incorporated and the unincorporated sectors. Effectively, average labour productivity is the average productivity change in both these sectors.
Labour productivity growth reflects growth in two areas. The first is from an increasing capital-labour ratio (capital deepening). That is, more capital per unit of labour input. The second is from increasing multifactor productivity. For example, the introduction of new disembodied technologies, organisational improvements, economies of scale, and the implementation of research and development. Unit labour costs will decrease as capital deepening and multifactor productivity increase.
More specifically, the ALC and the ALP expressions are:
(6) 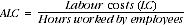
(7) 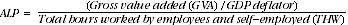
(8) 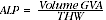
An apparent issue in the ULC formula is that the scope of the denominator, which includes the self-employed, is broader than the scope of the numerator. Equation 9 provides an alternative formulation to show that average labour costs are implicitly assumed to be the same for the self-employed as those for employees. Equation 6 shows ALC is measured for employees only. Using equations 5 and 7, total hours worked by employees and the self-employed can be shifted to the numerator in the ULC equation. The numerator in equation 9 then shows employee labour costs (LC) multiplied by the ratio of total hours worked to employee hours worked. Equation 9 shows the denominator remaining referenced to the whole economy and the numerator also has the same scope by factoring up the known labour costs for employees by the ratio of total hours worked to hours worked by employees. The implicit assumption in both equation 9 and equation 5 above is that the average hourly labour costs of the self-employed are the same as employees.
(9) 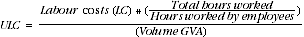
It is important to recognise that ULC as formulated here covers more than just the costs of employing employees. Nonetheless, since the costs applied to the self-employed are assumed to be the same as for employees the ULC derived is likely to be applicable to the case of employees only.
The LPI, AWE and average COE are different representations of average labour costs, with differing purposes. However, none take into account completely the effect that productivity has on reducing labour costs in terms of the cost per unit of output. The ULC adjusts ALC for the effects of productivity.
The choice of what is the most appropriate measure of ALC is one that is both practically and conceptually consistent. The LPI is ruled out because it is not conceptually consistent with labour productivity due to the compositional effects affecting labour productivity but not the LPI. While there are similarities between AWE and average COE, the choice of COE is more appropriate as it fits within the National Accounts framework that includes GVA. Further, the choice for ALC is COE per hour rather than per employee.
REAL UNIT LABOUR COSTS (RULC)
Nominal unit labour costs are subject to general increases in prices across the economy due to the numerator reflecting nominal labour costs. Real unit labour costs (RULC) are often used to eliminate this issue by deflating ALC with the GDP deflator. This provides an indicator that focuses more specifically on the direct labour cost pressures associated with the employment of labour, which excludes general price impacts. Below is a decomposition of real unit labour costs.
(10) 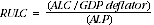
Substituting equation 7 into 10, the GDP deflator cancels out and this reduces the expression to:
(11) 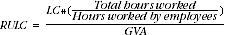
The labour income share (LIS) is defined as labour income (COE) divided by total factor income. The above formula shows that the RULC is similar in representation, but not identical to the labour income share. This is because the denominator for RULC, GVA, is slightly larger than the denominator for LIS, total factor income. If RULC is equated to the LIS, then equation 4 shows that the RULC can be placed within a broader theoretical framework defining the link between wages and productivity.
ULC MEASUREMENT ISSUES
Choice of price deflator
In calculating RULC measures the question arises as to the most appropriate deflator to use when calculating real labour costs. The issue does not exist when considering nominal ULC as labour costs are not deflated and volume GVA must be calculated by using the GDP deflator (see equation 8). Possible deflators to consider for real labour costs are the GDP deflator, GDP chain price index, domestic final demand (DFD) and household final consumption expenditure (HFCE).
When deciding the appropriate deflator it should be the case that it is representative of prices that the producer faces for output. This price gives an accurate measure of real labour costs as opposed to measuring the purchasing power of wages. Currently, the GDP implicit price deflator is preferred as its scope directly relates to the production of goods and services. Alternative measures such as the domestic final demand (DFD) deflator and the household final consumption expenditure (HFCE) deflator provide a demand side view of price change, which is less relevant in this situation.
Terms of trade effect on real unit labour costs
Australia's terms of trade (the ratio of export to import prices) has been increasing over recent years. As the terms of trade increases, the GDP deflator will also rise. There has been concern expressed that by using a GDP deflator in the derivation of RULC, growth in RULC may be masked to the extent that the GDP deflator overstates the growth in prices faced by domestic producers.
In the short run the important cost factor facing employer's ability to meet their wage bill is the actual domestic value of production rather than their purchasing power equivalent. For this reason, it may be the case that the DFD price deflator may be favourable in the unit labour cost equation, as this relates to domestic demand. That is not to say, that a judgement as to the capacity of the economy to pay higher wages should not recognise the consequences of a sustained shift in the terms of trade. However, if the interest is in the influence of labour costs on business decisions, then including the terms of trade effects can be inappropriate (Treasury 1978).
While it is true that for some producers who compete against the relatively cheaper imports the GDP deflator may not be ideal, it is also the case that for exporting producers they do see a relative increase in prices for their outputs. Overall, the GDP deflator continues to be the most appropriate broad measure of price change as it affects domestic producers and hence, even in times when the terms of trade are changing rapidly, the RULC should still be compiled using the GDP deflator.
Treatment of self employed
The estimate of ULC includes an estimate for the cost of self-employed labour by assuming that the self-employed earn, on average, the same amount per hour as employees. It would be preferable to determine an appropriate return to labour from within an overall measure of gross mixed income (GMI), the national accounts aggregate that measures returns to unincorporated businesses including the self employed. However, such a calculation requires too many assumptions for ULC compilation purposes and is not considered further here.
More critically, if the purpose of the ULC is to examine the costs of employees, that is, an employers' willingness to employ, then the returns to the self-employed should be excluded. However, in order to implement this in the overall ULC formula it is necessary to remove the self-employed component from both the numerator and the denominator in equation 9. While this is trivial for the numerator, it is not possible to define volume GVA excluding the self-employed.
Despite this limitation on the ULC formulation, since the implicit assumption is that the earnings of the self employed per hour are the same as for employees, there should be very little impact on the overall interpretability of the ULC results due to the inclusion of the self-employed.
ANALYSIS OF DATA
The data presented here highlights some of the various wage measures and their movements. The focus is on the ULC and the RULC. Figure 1 shows four basic wage measures, compensation of employees (COE) per hour, COE per employee, the Wage Price Index (WPI) and average weekly earnings (AWE). The WPI was chosen in preference to the labour price index because it is compiled on a quarterly basis. The figure shows that the WPI is less volatile than the other measures. The chart shows that the WPI has grown the slowest with the AWE growing fastest.
The data also show some volatility in movements from one quarter to the next. Care should be taken in interpreting movements between quarters of the ULC as a number of variables could explain any movements. Further movements in productivity over the short term can be ascribed to a number of effects not directly shown in the data, capacity utilisation and capital deepening are just two examples. Changes in productivity are generally analysed over longer time periods to examine changes in trends in productivity growth.
Figure 1. Selected wage related measures, Index 2003-04 = 100
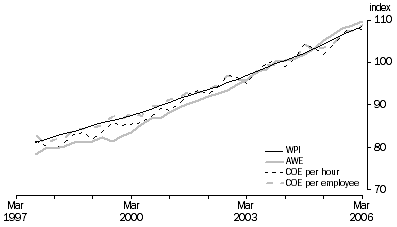
A comparison of growth rates between COE per hour and the WPI shows little difference in growth rates between the September 1997 quarter and September 2005 quarter, where both grew at the rate of 3.4 per cent per year. However, there were some divergences over this period, such as between September 2004 and September 2005 where the WPI grew by 4.1 per cent per year and the COE per hour by 2.4 per cent per year. Much of the divergences were due to quarter on quarter changes in total hours worked, as quarter on quarter growth in COE was relatively steady between 1.5 to 2.0 per cent. The WPI is not affected by changes in hours worked and as such is not as volatile as COE per hour.
UNIT LABOUR COSTS
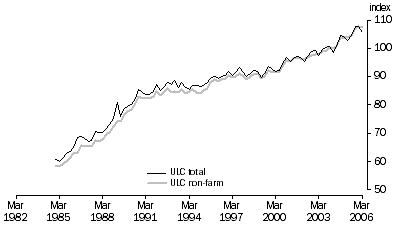
Figure 2 presents data on the ULC for the total economy and the non-farm sector. The non-farm sector is preferable as it removes some of the fluctuations associated with Agriculture. The chart shows similar movements in the non-farm and economy-wide estimates of ULC, but the non-farm movements are not as pronounced as the economy-wide estimates.
Over the last two decades non-farm ULC grew faster, at 2.8 per cent per year, compared to economy-wide ULC, which grew at 2.6 per cent per year (table 1). The difference driving the gap between the measures is due to differences in growth between total GDP and non-farm GDP as well as between total employee hours worked and non-farm employee hours worked.
Figure 2 shows that much of the growth in the ULC occurred in the second half of the 1980s. Little growth occurred over most of the 1990s and the ULC began rising again after 2000. Growth in the ULC over the second half of 1980s reflects higher growth in COE per hour at 4.5 per cent per year, than in GDP per hour, which grew by 0.9 per cent per year. The slower growth of ULC over the 1990s is because GDP per hour grew faster than in the latter half of the 1980s at 2.9 per cent per year and COE per hour's growth was slightly slower, at 3.8 per cent per year. The increase in ULC from 2000 is due to growth in GDP per hour slowing to 1.3 per cent per year, with growth in COE per hour remaining relatively unchanged since the 1990s (see table 1).
Figure 2. Unit labour costs, Index 2003-04 = 100
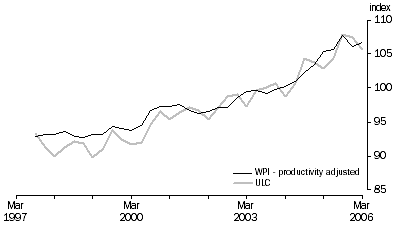
The previous section stated that the WPI does not take into account other productivity influences on wages. Figure 3 presents a labour productivity adjusted measure of WPI. There is no conceptually consistent productivity measure to adjust the WPI as this would require construction of a labour productivity measure that is not affected by compositional change. However, the purpose here is to show that labour productivity does have an influence on wages as the figure shows that the productivity-adjusted WPI has similar long term movements to the ULC.
The gap between the ULC and the adjusted WPI is representative of the difference between COE per hour and the WPI. That is, to some extent it illustrates the compositional effects in COE and hours worked.
Figure 3. ULC and productivity adjusted WPI, Index 2003-04 = 100
REAL UNIT LABOUR COSTS AND LABOUR INCOME SHARE
Figure 4 presents two estimates of RULC, an economy-wide and a non-farm estimate. While there are similar movements between the two series, there is somewhat less volatility in the non-farm series. Trends in the RULC are in the opposite direction to those of the ULC (figure 2). This is apparent over the second half of the 1980s and after 2000 where the RULC declines significantly compared to the ULC, which increases over these two periods.
In figure 4 the RULC is the ULC deflated by the GDP price deflator. The general decline in the RULC indicates that even though the nominal ULC was rising, the GDP deflator was increasing more quickly.
Figure 4. Real unit labour costs, Index 2003-04 = 100
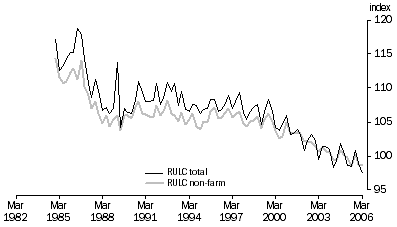
Figure 5. Real unit labour costs, using different deflators - Index 2003-04 = 100
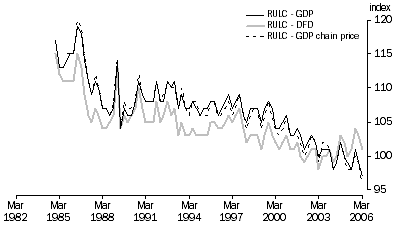
Figure 6. Non-farm RULC and labour income share, Index 2003-04 = 100
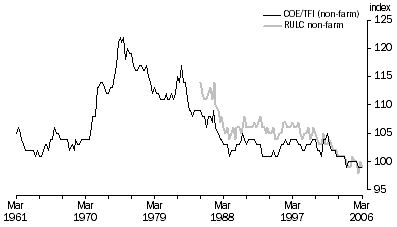
Figure 5 provides an indication of the effect of using a different deflator to estimate the RULC. There is very little difference between the GDP deflator and the GDP chain price index. The figure shows that using the DFD deflator the fall in the RULC is slower for much of the period from December 1984. However, since 2003 the DFD-deflated RULC appears to have increased.
Figure 6 shows the labour income share for the non-farm sector, defined here as COE divided by Total Factor Income (TFI). The figure shows the similarities in patterns since the mid-1980s between the RULC and the labour income share. However, the labour income share did not decline as rapidly as the RULC, especially over the last 5 years. The RULC declined by 0.8 per cent per year (table 1) from June 2000 to June 2005, while the labour income share declined by only 0.6 per cent per year at the economy-wide level.
Table 1 presents growth rates for the wage related indexes and includes the variables for the ULC. The table highlights that growth in ULC equals growth in COE per hour less growth in average labour productivity.
Growth rates for wage related indexes(a) |
|  |
 |  | June 1985 to June 1995 | June 1995 to June 2000 | June 2000 to June 2005 | June 1985 to June 2005 |  |
 |  | % p.a. | % p.a. | % p.a. | % p.a. |  |
|  |
| Total economy |  |  |  |  |  |
 | Compensation of employees per hour | 4.5 | 3.8 | 3.8 | 4.2 |  |
 | Average labour productivity(b) | 0.9 | 2.9 | 1.3 | 1.5 |  |
 | Unit labour costs | 3.5 | 0.9 | 2.5 | 2.6 |  |
 | GDP price deflator | 4.1 | 1.5 | 3.6 | 3.3 |  |
 | Real unit labour costs | -0.6 | -0.6 | -1.1 | -0.7 |  |
 | Wage price index(c) | na | 2.9 | 3.6 | na |  |
| Non-farm |  |  |  |  |  |
 | Compensation of employees per hour | 4.4 | 4.0 | 3.8 | 4.2 |  |
 | Average labour productivity(b) | 0.7 | 2.7 | 1.1 | 1.3 |  |
 | Unit labour costs | 3.7 | 1.2 | 2.7 | 2.8 |  |
 | GDP price deflator | 4.2 | 1.7 | 3.5 | 3.4 |  |
 | Real unit labour costs | -0.5 | -0.5 | -0.8 | -0.6 |  |
|  |
| na not available |
| (a) Growth rates based on log differences. |
| (b) GDP per hour. |
| (c) From June 1998. |
CONCLUSION
The different measures of labour cost discussed in the paper are required for the planning, evaluation and monitoring of economic and social development. The different users and uses of these statistics mean that a single all encompassing measure cannot satisfy all needs and that different measures need to be interpreted carefully in different situations.
This article has focused on the measurement of unit labour costs (ULC). Real ULC are measures that take into account productivity and general inflation when measuring average labour costs. By taking into account these factors a ULC measure indicates whether 'excess' labour cost growth may create cost pressures within the economy.
The theory and results presented here indicate that a ULC measure for Australia gives results similar to the WPI adjusted for labour productivity with the differences being mostly due to the compositional effects. By using COE per hour as the measure of average labour costs, the ULC is compositionally consistent between labour costs and productivity. The results indicate a broad consistency in the various labour cost measures over the past eight years.
While the ULC overcomes the consistency problem due to compositional changes, there are a few issues that also need accounting for, such as the choice of price deflator to estimate the RULC, whether the terms of trade should be taken into account in such a decision, and whether the labour income of the self-employed should be excluded. The article concludes that the GDP deflator is appropriate for deriving RULC measures and that no adjustment to exclude the impact of the self-employed is justified at present.
Historically, measures of nominal and real ULC have been compiled by the Commonwealth Treasury. Given the usefulness of ULC measures in the analysis of labour costs the ABS is planning to compile and release the ULC and the RULC defined here as part of its quarterly national accounts release commencing in September quarter 2006. The ABS will also continue to consider improved ways of measuring labour costs.
Questions and comments on the measurement of unit labour costs should be directed to Mr Paul Roberts on 02 6252 5360 or email paul.roberts@abs.gov.au.
REFERENCES
Australian Bureau of Statistics (ABS) 2006, Labour Statistics: Concepts, Source and Methods (cat. no. 6102.0.55.001), ABS, Canberra (accessed at www.abs.gov.au)
Commonwealth Dept of Treasury, 1978 'The measurement of real unit labour costs' Economic Roundup, Special Supplement, Canberra, September pp15 - 26.
Parham, D. Barnes, P. Roberts, P. and Kennet, 2000, Distribution of the Economic Gains of the 1990s, Staff Research Paper, AusInfo, Canberra, November.
 Print Page
Print Page
 Print All
Print All