TECHNICAL NOTE DATA QUALITY
RELIABILITY OF THE ESTIMATES
1 Since the estimates in this publication are based on information obtained from a sample, they are subject to sampling variability. That is, they may differ from those estimates that would have been produced if all dwellings had been included in the survey. One measure of the likely difference is given by the standard error (SE), which indicates the extent to which an estimate might have varied by chance because only a sample of dwellings (or households) was included. There are about two chances in three (67%) that a sample estimate will differ by less than one SE from the number that would have been obtained if all dwellings had been included, and about 19 chances in 20 (95%) that the difference will be less than two SEs.
2 In contrast to most other ABS surveys, PIAAC estimates also include significant imputation variability, due to the use of multiple possible assessment tasks and the complex scaling procedures. The effect of this on the estimation can be reliably estimated and is
included in the calculated SEs. An accepted procedure for estimating the imputation variance using plausible values is to measure the variance of the plausible values (with an appropriate scaling factor) as follows:
3 Together, the sampling variance and imputation variance can be added to provide a suitable measure of the total variance, and total SE. This SE indicates the extent to which an estimate might have varied by chance because only a sample of persons was included, and/or because of the significant imputation used in the literacy scaling procedures.
4 Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate:

5 Sampling error for estimates from PIAAC 2011-2012 have been calculated using the Jackknife method of variance estimation. This involves the calculation of 60 'replicate' estimates based on 60 different subsamples of the obtained sample. The variability of estimates obtained from these subsamples is used to estimate the sample variability surrounding the estimate.
6 A data cube (spreadsheet) containing tables produced for this publication and the calculated RSEs for each of the estimates is available from the Downloads tab of the publication.
7 Only estimates (numbers and proportions) with RSEs less than 25% are considered sufficiently reliable for most purposes. Estimates with RSEs between 25% to 50% have been included and are annotated to indicate they are subject to high sample variability and should be used with caution. In addition, estimates with RSEs greater than 50% have also been included and annotated to indicate they are considered too unreliable for general use. All cells in the data cube with RSEs greater than 25% contain a comment indicating the size of the RSE. These cells can be identified by a red indicator in the corner of the cell. The comment appears when the mouse pointer hovers over the cell.
CALCULATION OF STANDARD ERROR
8 SEs can be calculated using the estimates (counts or proportions) and the corresponding RSEs. For example, the estimated number of persons in Australia aged 15 to 74 years that have scores at Level 3 on the literacy scale is 6,379,600 and the RSE for this estimate is 1.8%. The SE is calculated by:
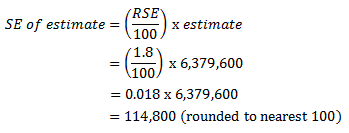
9 Therefore, there are about two chances in three that the actual number of persons that have scores at Level 3 on the literacy scale is in the range of 6,264,800 to 6,494,400 and about 19 chances in 20 that the value was in the range 6,150,000 to 6,609,200. This example is illustrated in the diagram below.

PROPORTION AND PERCENTAGES
10 Proportions and percentages formed from the ratio of two estimates are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. A formula to approximate the RSE of a proportion is given below. The formula is only valid when the numerator is a subset of the denominator:
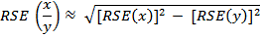
The RSEs of proportions within the data cubes have been provided. Calculations of RSEs for other proportions using the above formula should be seen as only indicative of the true RSE.
11 The proportion of Australians aged 15 to 74 who have scores at Level 3 on the literacy scale is 39% and the associated RSE is 2.4%. Therefore, the SE is 0.9 percentage points ((2.4/100) x 39). Hence there are about two chances in three that the proportion of Australians aged 15 to 74 years who have scores at Level 3 on the literacy scale is between 38.1% and 39.9%, and 19 chances in 20 that the proportion is between 37.2% and 40.8%.
DIFFERENCES
12 Published estimates may also be used to calculate the difference between two survey estimates (numbers or proportions). Such an estimate is also subject to sampling error. The sampling error of the difference between two estimates depends on their SEs and the relationship (correlation) between them. An approximate SE of the difference between two estimates (x-y) may be calculated by the following formula:

13 This formula will only be exact for differences between separate and uncorrelated characteristics or sub populations and only provides an indication for the differences likely to be of interest in this publication.
SIGNIFICANCE TESTING
14 A statistical significance test for any comparisons between estimates can be performed to determine whether it is likely that there is a difference between two corresponding population characteristics. The approximate standard error of the difference between two corresponding estimates (x and y) can be calculated using the formula in paragraph 12. The standard error is then used to create the following test statistic:
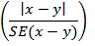
15 If the value of this test statistic is greater than 1.96 then there is evidence, with a 95% level of confidence, of a statistically significant difference in the two populations with respect to that characteristic. Otherwise, it cannot be stated with confidence that there is a real difference between the populations with respect to that characteristic. Any calculations using the above formula should be seen as only indicative of a statistically significant difference.
 Print Page
Print Page
 Print All
Print All
 Quality Declaration
Quality Declaration