TECHNICAL NOTE DATA QUALITY
INTRODUCTION
1 Since the estimates in this publication are based on information obtained from occupants of a sample of dwellings, they are subject to sampling variability. That is, they may differ from those estimates that would have been produced if all dwellings had been included in the survey. One measure of the likely difference is given by the standard error (SE), which indicates the extent to which an estimate might have varied by chance because only a sample of dwellings was included. There are about two chances in three (67%) that a sample estimate will differ by less than one SE from the number that would have been obtained if all dwellings had been included, and about 19 chances in 20 (95%) that the difference will be less than two SEs. Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate.
2 Due to space limitations, it is impractical to print the SE of each estimate in the publication. Instead, a table of SEs is provided to enable readers to determine the SE for an estimate from the size of that estimate (see table T1). The SE table is derived from a mathematical model, referred to as the 'SE model', which is created using data from a number of past Labour Force Surveys. It should be noted that the SE model only gives an approximate value for the SE for any particular estimate, since there is some minor variation between SEs for different estimates of the same size.
CALCULATION OF STANDARD ERRORS
3 An example of the calculation and the use of SEs in relation to estimates of people is as follows. Table 2 shows that the estimated number of people who were part-time employees in their main job in Australia was 2,638,300. Since this estimate is between 2,000,000 and 5,000,000, table T1 shows the SE for Australia will be between 17,050 and 28,450 and can be approximated by interpolation using the following general formula:
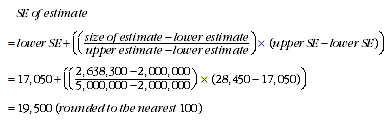
4 Therefore, there are about two chances in three that the value that would have been produced if all dwellings had been included in the survey will fall in the range 2,618,800 to 2,657,800, and about 19 chances in 20 that the value will fall within the range 2,599,300 to 2,677,300. This example is illustrated in the diagram below.

In general, the size of the SE increases as the size of the estimate increases. Conversely, the RSE decreases as the size of the estimate increases. Very small estimates are thus subject to such high RSEs that their value for most practical purposes is unreliable. In the tables in this publication, only estimates with RSEs of 25% or less are considered reliable for most purposes. Estimates with RSEs greater than 25% but less than or equal to 50% are preceded by an asterisk (e.g.*3.4) to indicate they are subject to high SEs and should be used with caution. Estimates with RSEs of greater than 50%, preceded by a double asterisk (e.g.**0.3), are considered too unreliable for general use and should only be used to aggregate with other estimates to provide derived estimates with RSEs of 25% or less. Table T2 presents the levels at which estimates have RSEs of 25% and 50%.
PROPORTIONS AND PERCENTAGES
6 Proportions and percentages formed from the ratio of two estimates are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. A formula to approximate the RSE of a proportion is given below. This formula is only valid when x is a subset of y.
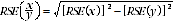 7
7 Considering the example above, of the 2,638,300 people who were part-time employees, 685,700 or 26% were men. The SE of 685,700 may be calculated by interpolation as 9,600. To convert this to an RSE we express the SE as a percentage of the estimate, or 9,600/685,700 = 1.4%. The SE for 2,638,300 was calculated previously as 19,500, which converted to an RSE is 19,500/2,638,300 = 0.7%. Applying the above formula, the RSE of the proportion is
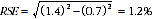 8
8 Therefore, the SE for the proportion of men who were part time employees, is 0.3 percentage points (=(26/100)x1.2). Therefore, there are about two chances in three that the proportion of men who were part time employees, is between 25.7% and 26.3% and 19 chances in 20 that the proportion is within the range 25.4% to 26.6%.
9 All other estimates produced from population estimates smaller than the values in T2 have RSEs larger than 25% and should be used with caution. T2 also indicates the size of the population estimates that would produce all other estimates with RSEs greater than 50% are considered too unreliable for general use.
DIFFERENCES
10 Published estimates may also be used to calculate the difference between two survey estimates (of numbers or percentages). Such an estimate is subject to sampling error. The sampling error of the difference between two estimates depends on their SEs and the relationship (correlation) between them. An approximate SE of the difference between two estimates (x-y) may be calculated by the following formula:
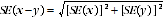 11
11 While this formula will only be exact for differences between separate and uncorrelated characteristics or subpopulations, it is expected to provide a good approximation for all differences likely to be of interest in this publication.
STANDARD ERRORS
T1 Standard Errors of Estimates |
|
 | NSW | Vic. | Qld. | SA | WA | Tas. | NT | ACT | Aust. |
| Size of estimate (persons) | no. | no. | no. | no. | no. | no. | no. | no. | no. | % |
|
| 100 | 290 | 290 | 220 | 180 | 220 | 110 | 80 | 100 | 110 | 110.0 |
| 200 | 400 | 380 | 320 | 240 | 290 | 160 | 120 | 170 | 190 | 95.0 |
| 300 | 470 | 440 | 390 | 280 | 340 | 190 | 150 | 210 | 260 | 86.7 |
| 500 | 580 | 540 | 500 | 340 | 420 | 240 | 200 | 270 | 380 | 76.0 |
| 700 | 660 | 620 | 580 | 390 | 480 | 270 | 230 | 300 | 480 | 68.6 |
| 1,000 | 760 | 710 | 680 | 450 | 550 | 310 | 270 | 330 | 610 | 61.0 |
| 1,500 | 900 | 830 | 810 | 530 | 640 | 360 | 320 | 360 | 780 | 52.0 |
| 2,000 | 1 010 | 930 | 910 | 590 | 710 | 390 | 350 | 390 | 920 | 46.0 |
| 2,500 | 1 100 | 1 000 | 1 000 | 650 | 800 | 400 | 400 | 400 | 1 050 | 42.0 |
| 3,000 | 1 200 | 1 100 | 1 050 | 700 | 850 | 450 | 400 | 450 | 1 150 | 38.3 |
| 3,500 | 1 250 | 1 150 | 1 100 | 700 | 900 | 450 | 400 | 450 | 1 250 | 35.7 |
| 4,000 | 1 300 | 1 200 | 1 200 | 750 | 900 | 500 | 450 | 450 | 1 350 | 33.8 |
| 5,000 | 1 450 | 1 300 | 1 250 | 800 | 1 000 | 500 | 500 | 500 | 1 500 | 30.0 |
| 7,000 | 1 650 | 1 500 | 1 450 | 900 | 1 150 | 600 | 600 | 600 | 1 700 | 24.3 |
| 10,000 | 1 850 | 1 700 | 1 600 | 1 050 | 1 300 | 700 | 750 | 700 | 2 000 | 20.0 |
| 15,000 | 2 150 | 1 950 | 1 800 | 1 200 | 1 500 | 850 | 1 000 | 850 | 2 350 | 15.7 |
| 20,000 | 2 400 | 2 200 | 1 950 | 1 350 | 1 650 | 1 000 | 1 300 | 1 000 | 2 550 | 12.8 |
| 30,000 | 2 800 | 2 550 | 2 250 | 1 550 | 1 900 | 1 250 | 1 800 | 1 250 | 2 900 | 9.7 |
| 40,000 | 3 100 | 2 800 | 2 500 | 1 800 | 2 100 | 1 500 | 2 300 | 1 500 | 3 150 | 7.9 |
| 50,000 | 3 350 | 3 050 | 2 750 | 2 000 | 2 300 | 1 700 | 2 750 | 1 650 | 3 400 | 6.8 |
| 100,000 | 4 250 | 4 000 | 3 750 | 3 000 | 3 400 | 2 400 | 4 750 | 2 250 | 4 300 | 4.3 |
| 150,000 | 5 000 | 4 850 | 4 600 | 3 850 | 4 450 | 2 850 | 6 500 | 2 500 | 5 000 | 3.3 |
| 200,000 | 5 750 | 5 650 | 5 400 | 4 550 | 5 350 | 3 200 | 8 150 | 2 650 | 5 600 | 2.8 |
| 300,000 | 7 250 | 7 250 | 6 850 | 5 550 | 6 750 | 3 700 | 11 150 | 2 800 | 6 650 | 2.2 |
| 500,000 | 10 150 | 10 050 | 9 250 | 7 000 | 8 600 | 4 250 | . . | 2 800 | 8 350 | 1.7 |
| 1,000,000 | 15 100 | 15 250 | 13 200 | 8 900 | 10 950 | 4 850 | . . | . . | 11 750 | 1.2 |
| 2,000,000 | 20 350 | 22 550 | 17 700 | 10 600 | 12 700 | . . | . . | . . | 17 050 | 0.9 |
| 5,000,000 | 25 900 | 36 100 | 23 900 | 11 900 | 13 250 | . . | . . | . . | 28 450 | 0.6 |
| 10,000,000 | 27 750 | 49 750 | 27 950 | . . | . . | . . | . . | . . | 37 950 | 0.4 |
| 15,000,000 | . . | . . | . . | . . | . . | . . | . . | . . | 42 850 | 0.3 |
|
| . . not applicable |
T2 Levels at which estimates have relative standard errors of 25% and 50%(a) |
|
 | NSW | Vic. | Qld. | SA | WA | Tas. | NT | ACT | Aust. |
 | no. | no. | no. | no. | no. | no. | no. | no. | no. |
|
| RSE of 25% | 6 300 | 5 400 | 5 100 | 2 600 | 3 500 | 1 400 | 1 100 | 1 400 | 6 800 |
| RSE of 50% | 2 000 | 1 800 | 1 700 | 800 | 1 200 | 500 | 300 | 600 | 1 600 |
|
| (a) Refers to the number of people contributing to the estimate. |
 Print Page
Print Page
 Print All
Print All
 Quality Declaration
Quality Declaration