APPENDIX 1 DETAILS ON METHODOLOGY
This appendix provides additional details on methodology and data sources that were discussed in Chapter 1 and Appendix 2.
CONCEPTS
Productivity is generally defined as the ratio of a measure of the volume output to a volume measure of input. Multifactor productivity (MFP) is defined as the ratio of output to two or more inputs, which is a relatively simple definition. However, the measurement of productivity is not straightforward. There are various complex issues involved in the measurement of output, input and other components used for deriving the MFP estimates. In fact, the reliability of an aggregate MFP measure for the whole economy is determined by how well the aggregate output, capital and labour and factor incomes are measured. These aggregates in turn depend on almost every aspect of the national accounts.
Moreover, there are various frameworks under which the MFP measure can be obtained. The same productivity measure under different approaches often uses different assumptions, and may give rise to different interpretations. Therefore there are two closely related issues involved in MFP estimation - the measurement issues and the issue of applying the appropriate method.
This appendix focuses on the methodology and the data sources used at the industry level, including measurement issues. The appendix will not present in detail the theoretical framework underpinning the methodology, or the issue of applying the appropriate method. For a treatment of the theoretical framework see Measuring Productivity: Measurement of Aggregate and Industry-level Productivity Growth, OECD Manual (OECD 2001a), Estimating Industry-level Multifactor Productivity for the Market-Sector Industries in Australia: Methods and Experimental Results (Zheng 2005), and Estimates of Multifactor Productivity, Australia (Aspden 1990).
The approach taken in this paper is based on the growth accounting framework established by Solow (1957). This provides for a derivation of the MFP measure based on an aggregate production function. This aggregate production function includes only one output and two types of aggregate input (although this could be extended to include intermediate inputs), capital and labour, with technology as an additional variable shifting over time.
MFP takes account of several factor inputs at the same time and is largely a measure of the effects of technical progress, improvements in the workforce, improvements in management practices, economies of scale and so on. MFP can also be affected in the short term to medium term by other factors such as weather and by variations in capacity utilisation. Strictly speaking MFP growth occurs when there is an upward shift in the production function.
This aggregate production function implies that all firms within the same industry have the same production function. Further, MFP in this framework measures disembodied technological change. That is, embodied technological change is captured in capital inputs and or intermediate inputs.
To estimate industry level MFP, indexes for volume measures of output, and primary and intermediate inputs are required, along with data on industry-level factor incomes. There are number of difficulties and measurement problems associated with industry-level MFP estimation. Some of these issues are addressed in this appendix.
OUTPUT AND INTERMEDIATE INPUTS
The gross outputs for each market sector industry in both volume and current price terms are obtained from the ABS supply-use tables that contain both market and non-market sector industries and more than two hundred commodity groups. Since 1994-95, the ABS has been compiling annual supply-use tables in both current price and volume terms. Thus, industry-level gross output MFP can be estimated from that period.
In the Australian supply-use framework, the current price gross output and value added are valued at basic prices. They exclude taxes payable and any transport charges paid separately by the producer, but include subsidies received, as a consequence of production or sale. The basic price is intended to measure the amount actually retained by the producer, the price most relevant to the decision-making process, and is therefore the price most appropriate for valuing output in productivity analysis.
The volume measures of gross output and intermediate inputs in the supply-use tables are derived from aggregation of supply and use commodities at constant prices. The volume supply and use commodities are estimated by deflating the nominal value of each commodity by the corresponding output and input price index. Thus, the corresponding volume measure of value added is based on the procedure of double deflation.
The series for industry level value added is much longer than that for gross output, although for years prior to 1994-95 the estimates were derived without using the supply-use framework.
To estimate value added for the years prior to 1994-95 it is assumed (for all industries other than Agriculture, forestry and fishing) that the volume measure of value added grows at the same rate as the volume measure of output (the output indicator method).
It is, therefore, implicitly assumed that gross output and intermediate inputs have the same growth rate. That is, there is no change in the efficiency of use of intermediate inputs in the production process. However, the efficiency of use of capital and labour will change.
For more details on how output is derived for individual industries see Australian System of National Accounts: Concepts, Sources and Methods (cat. no. 5216.0, ABS 2000).
CAPITAL INPUT
Capital services produced by an asset over its life are directly proportional to the productive capital value of the asset. By weighting together volume indexes of the productive capital stock of different assets using their rental prices as weights, an aggregate index of capital services is produced.
Estimates of productive capital stock for the following asset types have been used in the ABS estimation of MFP:
- six types of machinery and equipment: computers and computer peripherals; electronic and electrical machinery and communications equipment; industrial machinery and equipment; motor vehicles; other transport equipment; and other plant and equipment
- buildings and structures other than dwellings
- livestock
- three types of intangible fixed assets: artistic originals; mineral exploration; and computer software
- inventories
- land.
Chapter 16 of
Australian System of National Accounts: Concepts, Sources and Methods (cat. no. 5216.0) provides a full description of the method used to derive the capital stock measures for the relevant components of gross fixed capital formation (that is, for all assets listed above except inventories and land). The method used to derive productive capital stock using age-efficiency profiles is also described.
Volume estimates for inventory items are obtained for all the market sector industries other than Communications, Finance and insurance; and Cultural and recreational services.
A benchmark estimate of agricultural land is obtained from the balance sheet, where the value for the reference period is chosen. The stock of agricultural land is treated as a non-depreciable asset and in volume terms the productive capital stock of agricultural land is assumed to remain constant over time.
For non-agricultural land, estimates for each industry are calculated by taking the balance sheet value for the reference year as a benchmark, and assuming that the growth rate is half that of the productive capital stock of non-dwelling construction. This approach recognises that changes in the capital services provided by land can accrue due to changes in the value of the building on it, but disproportionately so.
An index of aggregate capital services is compiled in the form of a Tornqvist index (that is, the weighted geometric mean of the component growth rates). The growth rates of productive capital stocks of each asset type are weighted together using estimates of the rental prices. Rental prices are generally unobservable because, for most capital, the owner is also the user, and are estimated using the user cost of capital equation (see Appendix 2 for details).
LABOUR INPUT
Indexes of hours worked are used to estimate labour input. The hours worked estimates are derived as the product of employment and average hours worked. Using an index of hours worked provides a better measure of labour input than using employment, because hours worked captures changes in paid and unpaid overtime worked, standard weekly hours, leave taken, and changes in the proportion of part-time employees. However, changes in the skill level of the labour force are not captured in hours worked, and as such are reflected in the industry productivity estimates. To obtain a measure of productivity that excluded the effect of changing skill levels, it would be necessary to adjust hours worked for changes in the composition of the labour force.
To adjust for changes in the composition of the labour force it would be necessary to examine factors that might cause changes to the labour inputs. For instance, changes in labour inputs could be due to such factors as changes in the level of educational attainment or the age distribution of the work force. However, these are difficult to quantify. At present, the ABS does not attempt to make such adjustments at the industry level.
EMPLOYMENT ESTIMATES
The employment estimates used to derive hours worked comprises all labour engaged in the production of goods and services, and include not only wage and salary earners but also:
- employers
- self-employed persons
- persons working one hour or more without pay in a family business or on a farm.
The annual figures are simple averages based on the available observations of employment levels during the year.
Industry estimates should be compiled with the objective of ensuring full consistency between estimates of industry employment and gross value added (ideally both sets of estimates would be derived from the same source for each industry). However industry employment data from business surveys are not considered of sufficient quality for use in production analysis. Consequently the labour force survey (LFS) employment estimates are used. These are compiled from The Labour Force, Australia (cat. no. 6203.0) and relate to the mid-month of the quarter, as there are no industry estimates for the first and last month of each quarter.
HOURS WORKED
Total annual hours worked are based on estimates of actual hours worked from the LFS. Total hours actually worked are observed in the LFS during the two week reference period of each month. However, the design of the LFS means that this two week reference period is only representative of 'one week' of each month. So, each reference period is assigned to one calendar week of the month. This provides 12 weeks of the year where total hours worked are observed.
Total hours worked in the remaining unobserved weeks of the year are imputed by interpolating linearly between the 12 observed weeks. Interpolation of the weeks at the beginning of January and at the end of December requires information on hours worked in the observed weeks of the previous December and the following January respectively.
Before total hours worked in a LFS reference period can be assigned to a calendar week, or be used as the basis of linear interpolation, they must be corrected for events such as public and school holidays. These non-random holidays tend to affect hours worked during the week containing the holiday rather than neighbouring weeks. Hours worked during a reference period affected by a non-random holiday may not be representative of hours actually worked in the assigned calendar week, nor will they be a good indicator of hours worked in neighbouring weeks. An estimate of the hours lost due to each observed non-random holiday can be made using intervention analysis.
Regression-ARIMA (Autoregressive Integrated Moving Average) intervention analysis is a technique that can be applied to estimate the effect of a known event on a regular time series. The parameter estimates from this type of analysis can be used to create a holiday corrected time series which excludes the impact of non-random holidays. Once these hours are appropriately accounted for, the holiday corrected estimates provide an appropriate basis for linear interpolation.
The corrected hours worked estimates still contain the effects of seasonal changes to hours worked from factors such as sick leave, annual leave and periods when hours worked tend to be high. The effects of seasonal factors on hours worked tend to be similar in neighbouring weeks, rather than being specific to one particular week.
The interpolation procedure results in an estimate of holiday-corrected total hours worked in each week of a year. To be representative of total hours actually worked in each week of the year, the hours lost due to non-random holidays need to be accounted for. For non-random holidays, which are regularly observed in the LFS reference periods, the holiday correction obtained from intervention analysis can be weighted to be used to estimate the hours lost in each observed week. Hours lost from unobserved holidays are based on similar observed holidays. For example, the correction for Christmas is based on the observed correction for Easter.
The estimates of total hours actually worked in each week of the year are summed to create an estimate of monthly, quarterly or annual total hours worked. If the period does not start on a Monday, or end on a Sunday, total hours worked in the start, and/or end, week are apportioned to reflect this.
In order to obtain annual hours worked by industry it is necessary to make some simplifying assumptions, recalling that industry detail in the LFS is only available at the mid-quarter months. This mid-quarter month information is used to estimate the proportion of total hours worked by people employed in each industry in each of these four months. These quarterly proportions are weighted together to provide an annual proportion of total hours worked for each industry. Applying this proportion to total annual hours worked by all employed people gives an annual hours worked estimate for each industry. This method implicitly assumes that the effects of holidays and other seasonal factors are constant across all industries. The ABS intends to investigate ways to improve this aspect of the methodology.
For more details on the hours worked methodology see Information Paper: Implementing New Estimates of Hours Worked into the Australian National Accounts (cat. no. 5204.0.55.003).
FACTOR INCOMES
Estimates of factor incomes are required to derive the shares of labour and capital input used to measure MFP on a value added basis. For MFP on a gross output basis, estimates of cost shares for labour, capital and intermediate inputs are required. The share of intermediate inputs in gross output can be directly obtained by the current price measures of gross output and intermediate inputs in the supply-use tables. This is, however, not the case for capital and labour, because there are various other expenditure/income items in the current price measure of value added. As an accounting identity value added at basic prices is the same as total factor income plus taxes less subsidies on production and imports. Total factor income consists of compensation of employees, gross operating surplus and gross mixed income.
In most work on MFP estimation, the measures of factor income are often used to directly derive the relevant factor income shares. To do this, gross mixed income needs to be allocated to capital and labour. Gross mixed income is the income that accrues to unincorporated enterprises owned by members of household, that is, to self-employed persons. Gross mixed income consists of two major components, wages, salaries and supplements of unincorporated enterprises and the gross operating surplus of unincorporated enterprises. However, this split is not readily identifiable in the data, and has to be apportioned appropriately.
GROSS MIXED INCOME
For the household sector, the labour and capital shares of income earned by unincorporated enterprises are subsumed into one national accounts aggregate: gross mixed income. The following procedure has been used to impute the labour and capital shares of this aggregate for each industry in the market sector.
An initial estimate of labour income is imputed by assigning to proprietors and unpaid helpers the same average compensation per hour received by wage and salary earners. An initial estimate of proprietors' capital income is derived by multiplying the household productive capital stocks for each industry and asset type by corporate rental prices. An implicit value of proprietors' gross mixed income is obtained by summing these two products:
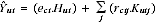
where
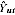 = the implicit value of proprietors' gross mixed income in industry i
= the implicit value of proprietors' gross mixed income in industry i
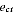 = the corporate average hourly compensation rate for wage and salary earners, industry i
= the corporate average hourly compensation rate for wage and salary earners, industry i
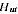 = total proprietors' hours worked
= total proprietors' hours worked
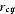 = the corporate rental price rate for industry i, asset type j
= the corporate rental price rate for industry i, asset type j
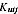 = household sectors' productive capital stock for industry i, asset type j
= household sectors' productive capital stock for industry i, asset type j
Final estimates are obtained by multiplying the average compensation per hour and the rental price component of by a scaling factor. This factor equates the sum of proprietors' capital and labour incomes to actual gross mixed income:
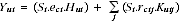
where the scaling factor 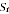 is:
is:
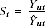
and 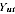 is actual gross mixed income.
is actual gross mixed income.
Proprietors' capital income for industry i is given by:
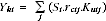
Proprietors' labour income is given by:
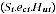
The proprietor's labour and capital income are added to the corporate sector's labour and capital income respectively to form total labour and capital income for the industry.
 Print Page
Print Page
 Print All
Print All