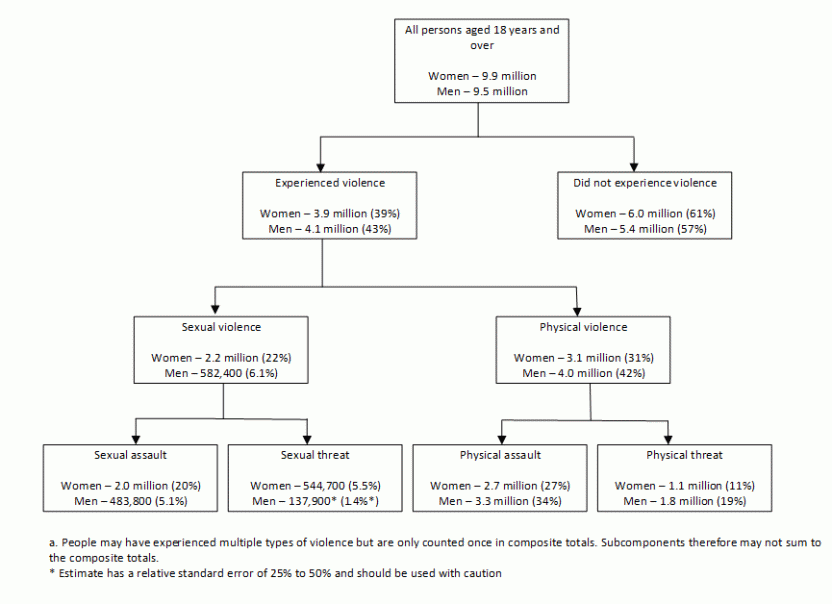
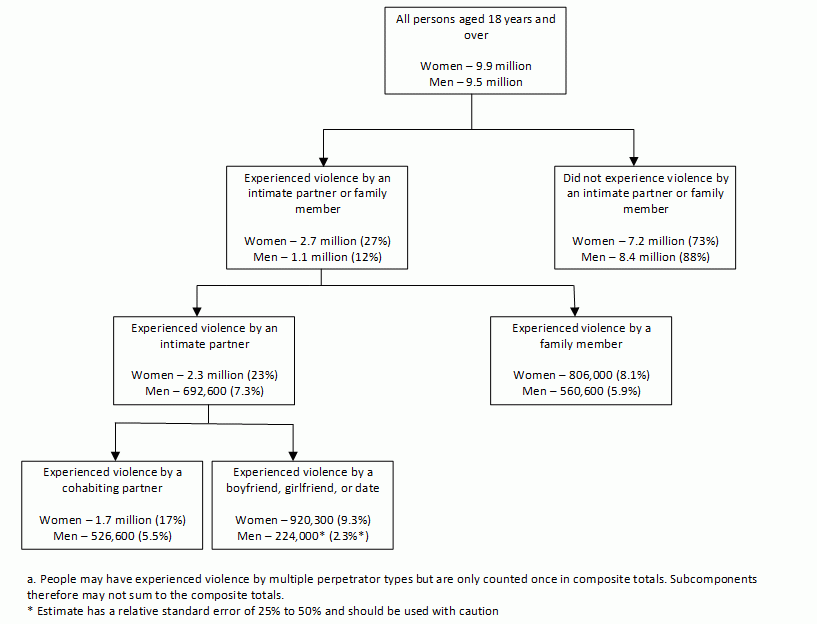
The Personal Safety Survey (PSS) collected information from persons aged 18 years and over about the nature and extent of their experiences of violence, including detailed information about experiences of:
- physical and sexual violence
- violence, emotional abuse, and economic abuse by a cohabiting partner
- stalking
- sexual harassment
- childhood abuse and witnessing parental violence before the age of 15
This publication presents high level prevalence statistics and changes over time for key violence types collected in the survey. For further detailed thematic publications using the PSS data refer to Related publications or follow the links in each chapter.
The ABS would like to thank those who participated in the survey and acknowledges the experiences of people affected by violence and abuse who are represented in this report.
Some people may find the contents of this report confronting or distressing. Support services are available: 1800RESPECT – 1800 737 732, Lifeline – 13 11 14.
COVID-19 context
The 2021-22 PSS was conducted between March 2021 and May 2022 during the COVID-19 pandemic. Throughout this time, government policies were in place to reduce the spread of COVID-19, including stay-at-home orders, border control measures, limits on gatherings, and social distancing rules. The survey results should be understood and interpreted within the broader context of the wide-ranging changes to everyday life during the pandemic.
Data quality and interpretation
In the written commentary, where a rate is described as higher or lower than a comparative rate, or one group is described as more or less likely to have had an experience than another group, the difference has been found to be statistically significant at the 95% confidence level.
Figures marked with an asterisk (*) have a relative standard error of between 25% and 50% and should be used with caution.
For more information about statistical significance and relative standard error, refer to the Personal Safety, Australia Methodology.