|
|
Technical Note: Data quality
ESTIMATION PROCEDURE
1 Estimates derived from this survey were obtained by adjusting the MPS selection weights to account for the survey taking a subsample of the dwellings selected for the MPS. The weights were then adjusted to ensure that the survey estimates conformed to an independently estimated distribution of the population (by number of adults and children within the household, and by part of the state) rather than the distribution among respondents.
2 The estimates were then obtained by summing the weights of households with the characteristic of interest. For example, an estimate of the total number of households with a security/burglar alarm is obtained by adding together the weight for each household in the sample with a security/burglar alarm.
RELIABILITY OF ESTIMATES
3 Estimates in this publication are subject to non-sampling and sampling errors.
Non-sampling errors
4 Non-sampling errors may arise as a result of errors in the reporting, recording or processing of the data and can occur even if there is a complete enumeration of the population. Non-sampling errors can be introduced through inadequacies in the questionnaire, non-response, inaccurate reporting by respondents, errors in the application of survey procedures, incorrect recording of answers, and errors in data entry and processing.
5 It is difficult to measure the size of the non-sampling errors and the extent of these errors could vary considerably from survey to survey and from question to question. Every effort was made in the design of this survey and in the development of survey procedures to minimise the effect of these errors.
Sampling errors
6 Sampling error is the difference between the published estimate, calculated from a sample of dwellings, and the value that would have been produced if all dwellings had been included in the survey.
7 One measure of the likely difference is given by the standard error (SE), which indicates the extent to which an estimate may vary from the true value. There are about two chances in three (67%) that a survey estimate is within one SE of the figure that would have been obtained if all households had been included in the survey, and about 19 chances in 20 (95%) that the estimate lies within two SEs.
8 Due to space limitations, it is impractical to print the SE of each estimate in the publication. Instead, a table of SEs is provided to enable readers to determine the SE for an estimate based on the size of that estimate (see table T1). The SE table is derived from a mathematical model, which is created using the data collected in the survey. The figures in the SE table will not give a precise measure of the SE for a particular estimate but will provide an indication of its magnitude.
9 Linear interpolation can be used to calculate the SE of estimates falling between the sizes of estimates presented in table T1, using the following general formula:
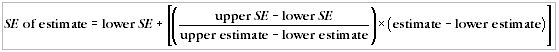
10 An example of the calculation and use of SEs is as follows. Table 10 shows that the estimated number of households in WA that had a security/burglar alarm installed was 216,000. Since this estimate is between 200,000 and 300,000, table T1 shows that the SE will lie between 6,750 and 7,800. The approximate value of the SE can be interpolated as follows:
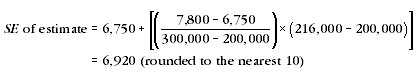
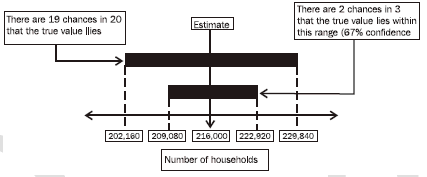
11 Therefore, there are about two chances in three that the true number of households in WA that had a security/burglar alarm installed lies between 209,080 and 222,920, and there are about 19 chances in 20 that the value lies between 202,160 and 229,840. This example is illustrated in the diagram below:
12 The SE can also be expressed as a percentage of the estimate, known as the relative standard error (RSE). The RSE is calculated by dividing the SE of an estimate by the estimate, and expressing it as a percentage. That is:

13 For example, the RSE for the number of households that had a security/burglar alarm installed is:
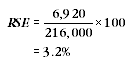
14 In general, the size of the SE increases as the size of the estimate increases. Conversely, the RSE decreases as the size of the estimate increases. Very small estimates are thus subject to high RSEs and are considered unreliable for general use.
15 Only estimates with an RSE of less than 25%, and percentages based on such estimates, are considered sufficiently reliable for most purposes. Estimates with RSEs greater than or equal to 25% have been included in this publication, however, they are preceded by a single asterisk when the RSE is 25% to 50% (e.g. * 3.3) and by a double asterisk when the RSE is greater than 50% (e.g. ** 0.9). A single asterisk indicates that the estimate is subject to high sampling error and should be used with caution. A double asterisk indicates that the estimate is considered too unreliable for general use.
16 Published estimates are sometimes used to calculate the difference between two survey estimates. Such an estimate is also subject to sampling error. The sampling error of the difference between two estimates depends on the SE of each estimate and the relationship (correlation) between them. The approximate SE of the difference between two estimates (x and y) may be calculated using the following formula:
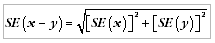
17 While this formula will only be exact for differences between separate and uncorrelated characteristics or subpopulations, it is expected to provide a good approximation for all differences likely to be of interest in this publication.
18 For example, Table 10 shows that an estimated 193,200 separate houses in WA and 18,400 semi-detached style households had a security/burglar alarm installed. This equates to a difference of 174,800 households. The standard error for each estimate is calculated using linear interpolation (as described above) and then the standard error on the estimate of the difference is calculated as:
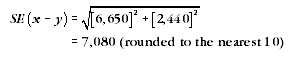
19 Therefore, there are about two chances in three that the true difference between the number of separate houses in WA and the number of semi-detached style households in WA that had a security/burglar alarm installed lies between 167,720 and 181,880, and there are about 19 chances in 20 that the value lies between 160,640 and 188,960.
T1 STANDARD ERRORS OF ESTIMATES OF WA HOUSEHOLDS |
|  |
 | SE | RSE |  |
Size of estimate
no. | no. | % |  |
|  |
| 500 | 320 | 63.8 |  |
| 700 | 400 | 56.5 |  |
| 1,000 | 490 | 49.4 |  |
| 1,500 | 630 | 42.1 |  |
| 2,000 | 750 | 37.4 |  |
| 2,500 | 850 | 34.0 |  |
| 3,000 | 950 | 31.5 |  |
| 3,500 | 1,050 | 29.4 |  |
| 4,000 | 1,100 | 27.7 |  |
| 5,000 | 1,250 | 25.0 |  |
| 7,000 | 1,500 | 21.4 |  |
| 10,000 | 1,800 | 18.0 |  |
| 15,000 | 2,200 | 14.7 |  |
| 20,000 | 2,550 | 12.7 |  |
| 30,000 | 3,050 | 10.2 |  |
| 40,000 | 3,500 | 8.7 |  |
| 50,000 | 3,850 | 7.7 |  |
| 100,000 | 5,150 | 5.2 |  |
| 150,000 | 6,050 | 4.0 |  |
| 200,000 | 6,750 | 3.4 |  |
| 300,000 | 7,800 | 2.6 |  |
| 500,000 | 9,300 | 1.9 |  |
| 1,000,000 | 11,550 | 1.2 |  |
|  |
|
 Print Page
Print Page
 Print All
Print All