- Butlin, N.G. (1962) Australian Domestic Product, Investment and Foreign Borrowing, 1861 - 1938/39. Cambridge: Cambridge University Press.
Haig, B.D. (1980) Capital Stock in Australian Manufacturing. Canberra: Department of Economics, Research School of Social Sciences, Australian National University.
Keating, M. (1967) The Growth and Composition of the Australian Workforce 1910-11 to 1960-61; thesis submitted to the Australian National University, Canberra.
Walters, R. and R. Dippelsman (1986) Estimates of Depreciation and Capital Stock, Australia. Occasional Paper 1985/3. Canberra: Australian Bureau of Statistics (ABS).
Walters, R. and R. Dippelsman (1986) Estimates of Depreciation and Capital Stock, Australia. Occasional Paper 1985/3. Canberra: Australian Bureau of Statistics (ABS).
OECD (2008) Frascati Manual: Proposed Standard Practice for Surveys on Research and Experimental Development. Paris: Organisation for Economic Co-operation and Development (OECD).
Winfrey, R. (1938) Statistical Analysis of Industrial Property Retirements. Ames, IA: Iowa State College of Agricultural and Mechanic Arts.
Sources and methods - Annual
The Perpetual Inventory Method (PIM)
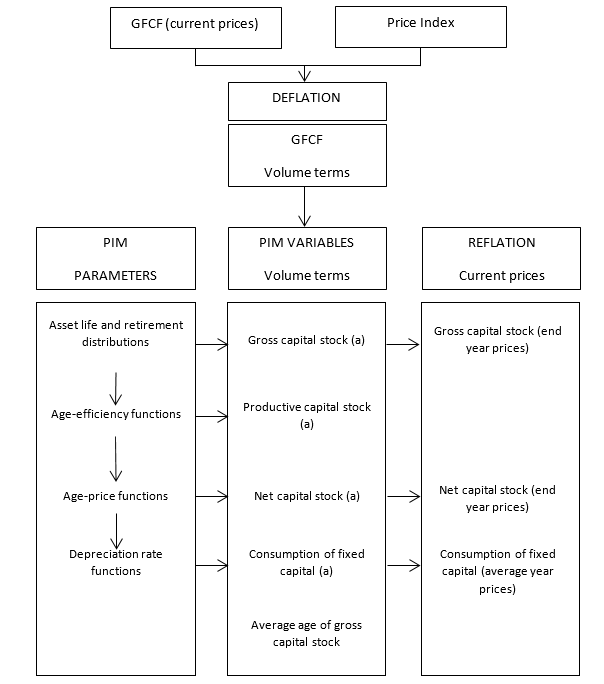
14.43 The PIM measures capital stock and COFC annually. The steps involved in applying the PIM are summarised in the chart below.
Figure 14.1 The PIM process
Image
Description
- Expressed in the average prices of the reference year
14.44 The PIM is applied to annual volume estimates of GFCF at a detailed level; that is, for a particular asset type for a particular industry in a particular institutional sector), in order to maintain an estimate of capital stock. It requires an initial estimate of capital stock, but this is taken to be zero. Volume estimates of net and productive capital stock and consumption of fixed capital are compiled using vector multiplication. The product of two vectors results in a value for a particular period. The first vector represents the age-efficiency or age-price or COFC pattern from when the fixed asset is new to the end of its life. The second vector is always the GFCF series. Shifting the second vector (GFCF) one year at a time before multiplying with the first vector results in a time series of values of capital stock or consumption of fixed capital, depending on the vector used.
14.45 For instance, gross capital stock at the end of period t is the product of the survival function and GFCF vectors. The first element of the GFCF vector is the value for period t; the second element is the value is for period t-1; the third is for period t-2; and so on. The final element is the value for period t-m, where m is the maximum possible life of the asset. A survival function represents the probability that a fixed asset is still in service and is derived from the asset life distribution. When the asset is new, the survival probability is equal to 1, but as it ages the survival probability declines, until it reaches zero. At the end of its life the asset is assumed to have a zero scrap value (in practice, it is recognised that positive and negative scrap values can occur but no attempt has been made to quantify the net effect of these). The survival function can be constructed by subtracting, for each period, the probability of retirement in that period.
14.46 Productive capital stock is the product of the average age-efficiency function (AAE) and GFCF vectors. The AAE for a particular asset age is calculated as a weighted average of the efficiency functions for each possible length of life, using the probability of retirement as weights.
14.47 Net capital stock is the product of the age-price function and GFCF vectors. Age-price functions are calculated using the AAE and a real discount rate in the following way. The present discounted value of the future stream of capital services from when the asset is new until the end of its life gives the first value of an age-price function, the present discounted value of the future stream of capital services from when the asset is one year old until the end of its life gives the second value, and so on. Age-price functions are normalised and adjusted on the assumption that all of GFCF in a year occurs mid-year.
14.48 COFC is the product of the depreciation rate function and GFCF vectors. The depreciation rate function is calculated as the decline in the age-price function between assets of consecutive ages.
14.49 Current price estimates at the most detailed level of estimation of gross capital stock, net capital stock and consumption of fixed capital are obtained by reflating the volume estimates. The price indexes used to reflate the volume estimates are the same as those initially employed to deflate GFCF except that, for capital stocks, they are adjusted to an end year basis by averaging consecutive values of the price indexes. For reflated consumption of fixed capital, which is a flow concept, the price indexes are not adjusted to an end of year basis. The resulting elemental series at current prices are aggregated to the level published, while elemental volume measures are aggregated to form chain volume measures at the level published. Elemental estimates of capital stock satisfy the following identities:
\(\large GKS_t = GKS_{t-1} + GFCF_t - R_t\)
\(\large NKS_t = NKS_{t-1} + GFCF_t - COFC_t\)
\(\large GKS$_t = (GKS_{t-1} + GFCF_t - Rt) * (PI_t + PI_{t+1}) / 2 \)
\(\large NKS$_t = (NKS_{t-1} + GFCF_t - COFC_t) * (PI_t + PI_{t+1}) / 2 \)
where
\(GKS_t=\) deflated gross capital stock in period \(t\)
\(NKS_t =\) deflated net capital stock in period \(t\)
\(GKS$_t =\) gross capital stock in current prices at end of period \(t\)
\(NKS$_t =\) net capital stock in current prices at end of period \(t\)
\(GFCF_t =\) deflated gross fixed capital formation in period \(t\)
\(R_t =\) deflated retirements in period \(t\)
\(COFC_t =\) deflated capital consumption in period \(t\)
\(PI_t =\) price index in period \(t\)
\($\) denotes the current dollar equivalent of the respective deflated series.
Note \(R_t\) is not included in the net estimates above as it is included in \(COFC\).
14.50 Average age of the gross capital stock at the end of each year is another output of the PIM. Average age is the age at 30 June of past years' GFCF weighted by their proportions of the surviving gross capital stock. These calculations assume an average mid-year purchase.
Current price GFCF
14.51 The GFCF data required as input into the PIM are consistent with those described previously, and are published in Australian System of National Accounts.
14.52 GFCF data by asset type are further classified by institutional sector and industry/purpose: dwellings; non-dwelling construction; machinery and equipment; cultivated biological resources; computer software; mineral and petroleum exploration; entertainment; literary or artistic originals; ownership transfer costs; research & development and weapons systems.
14.53 A number of problems with the generation of detailed capital formation estimates affect the reliability of estimates produced by the PIM. In particular, sector and industry estimates of private GFCF on machinery and equipment should be interpreted cautiously because the data available to adjust estimates in accordance with Australian Accounting Standard AASB16 and AASB117 (Accounting for Leases) are not as detailed as ideally required.
14.54 The first years for which estimates of capital stock and COFC have been published are 1966-67 and 1948-49, respectively. 1948-49 is the first year for which most national accounts data have been compiled by the ABS. Although the national accounts are compiled from 1959-60, in order to estimate capital stock and consumption of fixed capital from 1966-67 and 1959-60, respectively, estimates of GFCF are required for much earlier years. The length of the detailed GFCF series required varies depending on the particular mean asset life and asset life distribution applicable to that series.
14.55 Estimates of GFCF for years prior to 1948-49 are generally less accurate than those since 1948-49. The early data have relatively little impact on the present estimates because of the retirement of older assets, and the rapid growth of the Australian economy since World War II.
14.56 Estimates for years prior to 1948-49 are prepared using various sources including Butlin⁴⁶, and ABS data from issues of Production Bulletins, Primary Industry Bulletins, Secondary Industry Bulletins, Finance Bulletins, Transport and Communication Bulletins, State Statistical Registers and Australian and State Year Books.
14.57 Estimates of general government capital stock and consumption of fixed capital are calculated using the PIM by government purpose category. Estimates by purpose are then transformed into industries to obtain general government capital stock and consumption of fixed capital by industry. As the relationship between the government purpose classification and the ANZSIC is complex, this can only be done on an approximate basis.
Price indexes
14.58 The price indexes used in the PIM are the same as those used in the preparation of chain volume estimates of GFCF. However, the latter, with the exception of non-produced fixed asset estimates, are only compiled as chain volume estimates back to 1985-86. They are then linked to previously compiled constant price estimates at base years generally five years apart.
14.59 In contrast, the volume estimates derived as a means of estimating the capital stock related statistics are compiled all in one piece. The same is true for the reflation to derive current price estimates and chain volume estimates. This process requires the compilation of continuous price indexes going much further back in time than those required for the gross domestic product account.
14.60 For all categories other than construction, the price indexes extend no further back than 1948-49, but for construction they extend much further back. For years prior to 1948-49, the following price indexes are used:
- Dwellings and non-dwelling construction other than roads - a general building price index derived from Haig for the years 1938-39 to 1948-49.⁴⁷ For the years 1866 to 1938-39, a price index derived from Butlin.
- Roads - a roads price index derived from Keating, and Bureau of Transport Economics data (1941-42 to 1947-48).⁴⁸
14.61 As with the GFCF data, the poorer quality of early data should be considered in the light of its small contribution to more recent capital stock levels. Furthermore, unlike GFCF, most price indexes tend to be reasonably highly correlated over time.
14.62 The underlying price indexes from which the GFCF price indexes are compiled relate to a number of different base periods because of the length of the time series required. For example, ABS price indexes with base years of 1953-54, 1959-60, 1966-67, 1974-75, 1979-80, 1984-85 and 1989-90 are used, as well as non-ABS price indexes prior to 1948-49 which have earlier base years. Therefore, it is necessary to splice the price indexes with different base periods on the basis of relationships in overlapping periods.
14.63 Each item is a hybrid of several series, although only one price index series results for individual items. For example, price indexes for the early 1950s are used which reflect the composition of GFCF in 1953-54 when the current price values of machinery and equipment purchased in 1949-50 are calculated. In the mid to late 1950s, indexes which reflect the composition of GFCF in 1959-60 are used, etc.
Mean asset lives
14.64 The mean asset lives are the most important of the parameters used in the PIM. Together with asset life distributions, and the age-efficiency functions, they determine when assets are retired from the gross capital stock, the net capital stock, and the rate of depreciation charged. Six main data sources are used to derive estimates of mean asset lives:
- implicit tax lives;
- weighted prescribed tax lives;
- asset lives used by businesses to calculate depreciation for their own purposes;
- survival rates for vehicles in the motor vehicle fleet derived from data on new vehicle registrations and the motor vehicle census;
- technical information on the operating lives of various types of machinery from manufacturers' specifications; and
- asset life estimates from other OECD countries.
Changes in asset lives over time
14.65 Asset lives are influenced by a large number of variables, which may either increase or decrease asset lives over time. These variables include changes in rates of use, technological advances and quality changes.
14.66 In the case of motor vehicles there is strong evidence that mean lives have increased over the past fifty years, and these increases have been incorporated in the PIM for estimating the capital stock.
14.67 It is possible that the lives of other classes of assets have also changed, but there is no conclusive evidence to demonstrate that this has occurred.
14.68 While the lives of particular classes of assets may change over time, the average life span of all capital equipment also changes as a result of the changes in the composition of capital formation. This effect has been captured to some extent by breaking expenditure on machinery and equipment down into six major classes, as outlined below:
- Computers and peripherals equipment, encompassing laptops, tablets, PCs, printers and mainframes
- Electrical and electronic equipment, encompassing power generating equipment, transformers, batteries, solar panels and security equipment
- Motor vehicles encompassing cars, trucks, utes or any other vehicle where the primary use is to be driven on public roads
- Industrial machinery and equipment encompassing forklifts, conveyers, compressors, processing machinery or any other specialised equipment used for the operations of a business or organisation
- Other transport equipment, encompassing trailers, boats, ships, trains, aircraft or any other vehicle used in the transportation of people or goods
- Other equipment, encompassing equipment not elsewhere classified in the categories above.
14.69 Since the 1960s, there has been a steady increase in the use of computers, which in 1997-98 comprised about 12 per cent of capital formation on machinery and equipment. Computers are a relatively short-lived item of equipment and the increase in their use has had the effect of reducing average equipment lives.
14.70 The increased use of computers and the increased lives of motor vehicles have offsetting effects, with the net impact on equipment lives differing between industries according to the relative weights of computers and motor vehicles in their machinery and equipment expenditure. In industries where motor vehicles form a high proportion of machinery and equipment expenditure, such as agriculture, average lives have increased, while for industries such as finance and insurance, where computers form a relatively high proportion of capital formation, average equipment lives have fallen.
Machinery and equipment
14.71 Asset lives are estimated for the six classes of machinery and equipment. In calculating average asset lives, implicit tax lives (based on the inverse of the depreciation rates published in the 1997 Master Tax Guide) are used as a basic source of information. While implicit tax lives may change over time, they are regarded as being of insufficient accuracy to calculate changes in economic lives over time. They are, however, industry based and comprehensive in coverage. In principle they are based on industry information about the actual service lives of machinery and equipment. Nevertheless, information from other sources suggests that tax lives are, in general, shorter than economic lives, and additional sources have been used to estimate the actual economic lives of the various types of machinery and equipment.
14.72 The additional information sources are less comprehensive in coverage than the tax data, so selected items of machinery and equipment have been used to estimate ratios of tax lives to economic lives. The general approach has been to calculate a weighted average tax life for the various types of machinery and equipment employed in each industry, then supplementary sources, such as technical data and information collected from industry sources have been used to estimate the economic lives of assets employed in those industries. The estimates developed by Walters and Dippelsman have been adopted where no new information on economic lives has been available.⁴⁹ A ratio of economic lives to average tax lives has then been calculated. This ratio has been applied to all machinery and equipment employed in the industry to determine an average economic life.
14.73 The ratio of economic lives to tax lives differs between industries. For example, much of the machinery and equipment used in agriculture is similar to machinery and equipment used in mining and construction, and particular items of machinery and equipment, such as tractors, generally have the same prescribed tax life regardless of the industry in which they are employed. However, work practices differ between industries, with machinery and equipment engaged in agriculture generally being used less intensively than similar equipment in the construction or mining industries. Therefore, agricultural equipment can be expected to last longer than similar equipment engaged in construction or mining, and so the ratio of economic lives to tax lives is higher for agriculture than for construction or mining. In some cases, the lives of particular classes of machinery and equipment differ between industries; this is notably so in the case of electrical equipment. In the electricity, gas and water industry, electrical equipment is estimated to have an average life of 30.9 years, compared with an average life of 16.6 years for electrical equipment in other industries. This difference is due to an allowance being made for the longer life of the heavy electrical equipment used in the electricity, gas and water industry.
14.74 Asset lives for machinery and equipment in 1996-97 are reported in the table below for each industry. Due to a lack of information as to whether asset lives have been lengthening or shortening, the asset lives of all categories other than road vehicles and computers are held constant.
14.75 In the case of road vehicles, which constitute over 30 per cent of GFCF on machinery and equipment, average lives have been estimated using data on new vehicle registrations and the age composition of the vehicle fleet. Data are published in New Motor Vehicle Registrations, Australia: Preliminary and Motor Vehicle Census, Australia. For the census years, the number of vehicles of each vintage surviving in the stock has been related to the number of new registrations in the year of manufacture to calculate the percentage of survivals from the respective vintages. The results show a general decline over time as the older vehicles drop out of the stock. The point at which 50 per cent of vehicles manufactured in a particular year remain in the stock gives the median life of vehicles manufactured in that year. For example, if 50 per cent of the vehicles manufactured in 1960 (or more precisely first registered in 1960) remain in the stock in 1972, then this implies that the median life of vehicles manufactured in 1960 is 12 years. This technique has been used to estimate vehicle lives at the census dates, and lives for the intervening years have been calculated by interpolation. It is not possible to precisely calculate mean lives, as a proportion of vehicles have lives exceeding the range covered by the data available. However, analysis of the age distribution suggests that the median is a close approximation to the mean.
14.76 Vehicle lives are estimated using the above approach from 1950. Motor vehicle lives increased from 13.9 years to 18.7 years over the period, 1950 to 1979. It is not possible to measure the median lives of vehicles manufactured until half of them have actually lived out their lifespan and so for recent years this method is not applicable. For recent years a combination of data for the average age of the vehicle fleet and trends in the age profile of the fleet are used to project trends in vehicle lives. It is estimated that the mean life of motor vehicles manufactured in 1997 is 19.9 years.
14.77 The average life of computer equipment is assumed to have gradually declined from 8.5 years in 1960 to 5.4 years in 1997-98. This change is attributed to the decline in the proportion of mainframe computers relative to PCs and the longer lives of the former.
14.78 The table below outlines the mean asset lives (years) for machinery and equipment (excluding weapons systems) by type of equipment and industry.
| Industry | Computers & peripherals | Electrical & electronic equipment | Industrial machinery & equipment | Motor vehicles | Other transport equipment | Other plant & equipment |
|---|---|---|---|---|---|---|
| Agriculture, forestry & fishing | 5.4 | 16.5 | 21.7 | 19.9 | 16.5 | 17.8 |
| Mining | 5.4 | 17.8 | 19.9 | 19.9 | 17.8 | 16.5 |
| Manufacturing | 5.4 | 13.9 | 15.6 | 19.9 | 13.9 | 12.6 |
| Electricity, gas, water & waste services | 5.4 | 30.9 | 20.6 | 19.9 | 18.7 | 17.8 |
| Construction | 5.4 | 13.9 | 15.6 | 19.9 | 13.9 | 12.6 |
| Wholesale trade | 5.4 | 18.7 | 20.6 | 19.9 | 18.7 | 17.8 |
| Retail trade | 5.4 | 18.7 | 20.6 | 19.9 | 18.7 | 17.8 |
| Accommodation, & food services | 5.4 | 18.7 | 20.6 | 19.9 | 18.7 | 17.8 |
| Transport, postal & warehousing | 5.4 | 18.7 | 20.6 | 19.9 | 18.7 | 17.8 |
| Information media, & telecommunications | 5.4 | 15.6 | 17.8 | 19.9 | 15.6 | 14.9 |
| Finance and insurance services | 5.4 | 15.6 | 17.8 | 19.9 | 15.6 | 14.9 |
| Rental hiring & real estate services | 5.4 | 15.6 | 17.8 | 19.9 | 15.6 | 14.9 |
| Professional, scientific and technical services | 5.4 | 15.6 | 17.8 | 19.9 | 15.6 | 14.9 |
| Administration & support services | 5.4 | 15.6 | 17.8 | 19.9 | 15.6 | 14.9 |
| Public administration & safety | 5.4 | 15.6 | 17.8 | 19.9 | 15.6 | 14.9 |
| Education and training | 5.4 | 17.8 | 19.9 | 19.9 | 17.8 | 16.5 |
| Health care and social assistance | 5.4 | 15.6 | 17.8 | 19.9 | 15.6 | 14.9 |
| Arts and recreation services | 5.4 | 17.8 | 19.9 | 19.9 | 17.8 | 16.5 |
| Other services | 5.4 | 17.8 | 19.9 | 19.9 | 17.8 | 16.5 |
Weapons systems
14.79 The ABS has undertaken research on asset lives and retirement functions for each equipment type (aircraft, ships, ground equipment) using asset life information from the Australian Defence Force (ADF).
14.80 The ADF determines the current service life by subtracting the inception date from the planned withdrawal date for different weapon sub classes and this is seen as a suitable estimate of asset lives.
| Mean life (years) | ||
|---|---|---|
| Weapons systems | 27.8 | |
Non-dwelling construction
14.81 The estimated average lifespans of non-dwelling construction (including alterations and additions) are given in the table below. These estimates are based on the findings of Walters and Dippelsman.
14.82 These estimates have been checked against data on the age of buildings demolished in the Sydney and Melbourne central business districts over a ten-year period. The Sydney and Melbourne data broadly support the age estimates used by Walters and Dippelsman (1985), giving an average age at demolition of 62 years.
14.83 The short time span for which data are available and the relatively small number of buildings demolished over that period do not permit any significant conclusions to be drawn as to whether building lives have been increasing or decreasing over time. It can be argued, a priori, that as a result of economic and population growth the use of core infrastructure becomes more intensive (i.e. the flow of services from that infrastructure increases) and that, all things being equal, the life span of those facilities would be reduced. However, in the absence of clear empirical evidence to support that proposition, the asset lives used by Walters and Dippelsman have been retained.
Private corporations
14.84 Taxation lives are considered too short and lacking in discrimination between different industries and types of buildings. Unpublished data used in compiling the ABS publication, Building Activity, Australia were obtained showing separately new work and alterations and additions for different types of buildings. Alterations and additions are assumed to have an average asset life about half that of new work in that they can occur at most stages in the life of the primary building. Information on types of other construction for the private sector is obtained from the ABS publication, Engineering Construction Activity, Australia. Estimates are finalised on a subjective basis, taking into account lives used in other OECD countries, accounting estimates, and estimated proportions of new buildings, alterations and additions and non-building construction.
Public corporations
14.85 For public corporations, separate investigations are undertaken for electricity, gas and water; transport and storage; communication; accommodation, cafes and restaurants, cultural and recreational services; and personal and other services. Mean lives for public corporations are also reported separately in the table below. Together, these industries account for around 90 per cent of public corporations GFCF. For other industries, the estimates of private sector asset lives are used.
General government
14.86 Non-dwelling construction consists mostly of offices, schools, hospitals and roads. The average life of total non-dwelling construction is estimated to be 54 years, with new government buildings assumed to have the same average life as private commercial buildings of 65 years. As with private commercial buildings, the evidence as to whether the average lives of buildings are changing over time is inconclusive, and lives are assumed to remain constant over time. For non-dwelling construction on roads the mean asset lives used by Walters and Dippelsman (1985) have been retained.⁵⁰
Dwellings
14.87 The initial estimates used by Walters and Dippelsman have been retained up until 1985. However, recent analysis of demolitions data suggest that asset lives have declined in recent years due to obsolescence likely resulting from increasing land prices and demand for well-located land. The ABS has gradually reduced the asset lives of private brick dwellings from 88.1 years to 70 years and Alterations and additions from 39.5 years to 25 years to reflect changes in the economy over this time.
Ownership transfer costs
14.88 The treatment for ownership transfer costs in the PIM is unique. The cost of ownership transfer is written off over the period during which the acquirer expects to hold the asset. If the expectation is met, the costs of ownership transfers will be entirely depreciated when the asset is resold.
14.89 The table below outlines the mean asset lives (years) for non-dwelling construction, dwellings and ownership transfer costs by industry and institutional sector.
| Financial and non-financial corporations | Public non-financial corporations and general government | |||
|---|---|---|---|---|
| NON-DWELLING CONSTRUCTION | ||||
| Agriculture, forestry & fishing | 41.8 | 41.8 | ||
| Mining | 29.5 | 29.5 | ||
| Manufacturing | 38.6 | 38.6 | ||
| Electricity, gas, water & waste services | 55.3 | n.a. | ||
| Electricity and gas | n.a. | 37.9 | ||
| Water and waste services | n.a. | 71.6 | ||
| Construction | 44.5 | 44.5 | ||
| Wholesale trade | 50.6 | 38.6 | ||
| Retail trade | 50.6 | 38.6 | ||
| Transport, postal & warehousing | 40.6 | n.a. | ||
| Urban transport | n.a. | 51.9 | ||
| Road and rail transport | n.a. | 67.0 | ||
| Sea transport | n.a. | 47.5 | ||
| Air transport | n.a. | 30.9 | ||
| Other transport, postal & storage services | n.a. | 49.1 | ||
| Information, media, & telecommunications | 40.6 | 49.1 | ||
| Accommodation & food services | 50.6 | 41.7 | ||
| Financial & insurance services | 57.3 | n.a. | ||
| Rental hiring & real estate services | 57.3 | 57.3 | ||
| Professional, scientific and technical services | 57.3 | 57.3 | ||
| Administration & support services | 57.3 | 57.3 | ||
| Public administration & safety | n.a. | 54.1 | ||
| Education & training | 50.6 | 50.6 | ||
| Health care and social assistance services | 50.6 | 50.6 | ||
| Arts and recreation services | 50.6 | 50.6 | ||
| Other services | 50.6 | 50.6 | ||
| General government (all industries except Defence and roads) | n.a. | 54.1 | ||
| Defence | n.a. | 38.6 | ||
| Roads | n.a. | 33.4 | ||
| DWELLINGS | ||||
| Private brick homes | 70.0 | n.a. | ||
| Private timber, fibro and other houses | 58.9 | n.a. | ||
| Private non-house dwellings (units, flats, etc.) | 58.9 | n.a. | ||
| Private alterations and additions | 25.0 | n.a. | ||
| Public | n.a. | 58.9 | ||
| OWNERSHIP TRANSFER COSTS | ||||
| Dwellings | 17.0 | n.a. | ||
| Non-dwelling construction | 30.9 | n.a. | ||
Cultivated biological resources
Livestock
14.90 Information about mean asset lives of breeding and dairy cattle, and wool producing sheep, were obtained from several industry bodies; namely, Bureau of Rural Sciences; Woolmark Company; Dairy Farmers Corporation; and Meat and Livestock Association. Asset lives used are: breeding cattle stock – mean seven years; dairy cattle – mean ten years; and sheep for wool – mean six years. The same method is used for thoroughbred horses, standardbred horses, other horses and pigs for breeding, due to the limited information available to calculate the asset lives of these biological resources.
Orchard growth
14.91 There are three components of capital estimates, namely, orchard fruit and nut trees, plantation fruit bearing plants, and grapevines. These have different asset lives due to the types of plants.
14.92 The table below outlines the mean asset lives (years) for cultivated biological resources.
| Mean life (years) | |
|---|---|
| Livestock | |
| Sheep (wool) | 6.4 |
| Dairy | 10.3 |
| Breeding cattle | 7.5 |
| Thoroughbred horses | 10.3 |
| Standardbred horses | 10.3 |
| Other horses | 10.3 |
| Pigs for breeding | 8.5 |
| Orchards | 29.5 |
| Plantations | 7.5 |
| Grapevines | 40.6 |
Intellectual property products
Research & development
14.93 The value of R&D capital depreciates over time as new innovations emerge. As this occurs, earlier R&D becomes less effective in the production process and contributes less to profitability. Because of the intangible nature of the asset, the decline in value is difficult to measure and most studies use a range of assumptions based on econometric studies or the observed retirement rates for patents. The Australian Industry Commission report on Research and Development (1995) cites work by Mansfield (1973) and Pakes and Shankerman (1978, 1984), suggesting that industrial knowledge depreciates faster than physical capital with little left after 10 years. More recent studies have suggested that the rate of technological change, and consequently the rate of obsolescence, has increased in recent years (Caballero and Jaffe, 1993). Data on patent expiry rates suggest considerably longer asset lives.
14.94 Data compiled by Intellectual Property Australia show that the mean lifespans of standard patents filed in Australia between 1980 and 2001 were between 10 and 13 years. The data are categorised by 'technology group', whereas R&D expenditure data are categorised by industry (to sub-division level). There is no simple correspondence between the technology group classification and the industry classification; however, there are relatively small differences between the mean patent lives for different technology groups. Given the difficulties in producing estimates for individual industries, and the fact that the estimates (based on the patent data) do not differ greatly, a single asset life distribution is used for all R&D in the ASNA. A mean asset life of 11.3 years has been derived from a weighted average of the patent lives of the different technology groups.
14.95 Patent lives do not necessarily represent the lives of all R&D products and, in principle, an adjustment should be made to account for the fact that not all R&D is patented. Although it seems reasonable to expect that non-patented R&D would on average have shorter lives and depreciate faster than patented R&D, empirical estimates based on econometric studies vary greatly (with some of the evidence suggesting a longer life than that estimated from patents). In the United States in 2007, the Bureau of Economic Analysis (BEA) tested four scenarios, with the first scenario based on a 15 per cent annual depreciation rate. The other scenarios were based on more rapid rates of technological change, and consequently more rapid rates of obsolescence. The assumption of shorter economic lives gives greater weight to more recent innovations in the capital stock estimates.
14.96 A mean asset life of 11.3 years is broadly consistent with international results. A recent draft OECD Handbook states that the different approaches to estimating R&D asset lives 'generally indicate that service lives lie between 10 and 20 years'.⁵¹ However, most countries have not committed to an estimate and/or method to be used in their national accounts (the US figures have been used in the BEA's R&D Satellite Account). None of the OECD countries use an asset life significantly shorter than 10 years. For many countries only a depreciation rate is specified, but under a standard double declining balance assumption (that is double that of a straight-line depreciation) they imply similar (or sometimes longer) lives. Given the lack of evidence to the contrary, the ABS has assumed a mean asset life of 11.3 years based on patents data.
Computer software
14.97 It is important to distinguish between the different types of software because they are known to have different asset lives, partly due to the different lives of mainframe and personal computers. The software 'mix' has also been changing over time, in favour of PC-based software.
- In-house and customised software – information has been obtained from academic papers and Gartner research, although empirical evidence is quite weak. For years up to 1988-89, a mean life of eight years has been chosen. From 1989-90, the greater incidence of outsourcing software development, combined with increased technological change, is believed to result in shorter lives, and so a mean life of 6.5 years has been used.
- Purchased (packaged) software – for years up to 1988-89, a mean life of six years has been chosen. From 1989-90, average and maximum lives fall by about 2 years to reflect the impact of greater technological change; thus, average lives fall from 6 to 4.5 years in 1989-90.
Entertainment, literary or artistic originals
14.98 Music – general information about the life cycle of typical Australian music titles is obtained from the Australian Record Industry Association (ARIA). Indications point to an average life of about 3 years. However, detailed information is not obtained from ARIA's membership to verify the accuracy of these indications.
14.99 Film and TV – it is difficult to attribute an asset life to film as little is known about the percentage of films that continue to generate revenue for periods greater than one year, two years etc. However, information from the Australian Film Commission, and from Martin Dale's book The Movie Game - the film business in Britain, Europe and America, indicated that an average life of 3.5 years would be appropriate.
14.100 Literary – information is obtained from the Australian Publishers Association's (APA) booklet, Introduction to Book Publishing, and from enquiries to large publishers. APA recognises that books have a very short life. An average life of 2.7 years was proposed, and there were no objections to this estimate in discussions with experts from the APA and other large publishers. However, the increasing availability of new print technology such as 'print on demand' could redistribute the author's income, and therefore the life of book titles, over a longer period in the future.
Mineral exploration
14.101 Asset lives for mineral exploration are assumed to coincide with mine and oilfield lives. These are derived indirectly using economic demonstrated resources (EDR) from the balance sheets. First, average annual production for each commodity is divided into its EDR to derive the asset life for each commodity. Using exploration expenditure proportions for each commodity as weights, the average lives for the commodities are aggregated to an average mine life for all commodities. The average mine life used for mineral exploration is 34.5 years.
14.102 Mine lives for some commodities, namely black coal, iron ore and uranium, have extremely long asset lives, and are excluded from the calculation to avoid distorting the average life. These items had a much greater proportion of total exploration expenditure in early years, but their inclusion would lead to an unjustifiably strong decline in the overall average life of mineral exploration over time.
14.103 The table below outlines the mean asset lives (years) for intellectual property products.
| Mean life (years) | ||
|---|---|---|
| Computer software | ||
| In-house & customised (a) | 6.5 | |
| Purchased (b) | 4.5 | |
| Artistic originals | ||
| Film & TV | 3.5 | |
| Music | 2.7 | |
| Literary | 2.7 | |
| Exploration | 34.5 | |
| Research & Development | 11.3 | |
a. Prior to 1989-90, the mean life is 8 years
b. Prior to 1989-90, the mean life is 6 years
Asset life distributions
14.104 The PIM is applied at a relatively high level of disaggregation, with each component of GFCF consisting of a large variety of individual assets, each with its own life span. Even within particular types of assets, variations in lives will occur because of differences in the rate of use, maintenance etc. Because of the lack of recent empirical evidence, asset life distribution curves developed by Winfrey in 1938 are used.⁵² The Winfrey S3 is a bell-shaped symmetric curve, with approximately three quarters of assets retiring within 30 per cent of the mean asset life. It is empirically based, related to variations in lives of particular types of assets, and is consistent with the general presumption that the expected life for a particular asset will follow an approximately normal distribution.