RELIABILITY OF THE ESTIMATES
1 Since the estimates in this publication are based on information obtained from occupants of a sample of dwellings, they are subject to sampling variability. That is, they may differ from those estimates that would have been produced if all occupants of all dwellings had been included in the survey. One measure of the likely difference is given by the standard error (SE), which indicates the extent to which an estimate might have varied by chance because only a sample of dwellings (or occupants) was included. There are about two chances in three (67%) that a sample estimate will differ by less than one SE from the number that would have been obtained if all dwellings had been included, and about 19 chances in 20 (95%) that the difference will be less than two SEs.
2 Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate:

3 In the tables in this publication, only estimates (numbers, percentages, means and medians) with RSEs less than 25% are considered sufficiently reliable for most purposes. However, estimates with larger RSEs have been included and are preceded by an asterisk (e.g. *3) to indicate they are subject to high SEs and should be used with caution. Estimates with RSEs greater than 50% are preceded by a double asterisk (e.g. **2) to indicate that they are considered too unreliable for general use.
4 Limited publication space does not allow for the separate indication of SEs and/or RSEs of all the estimates in this publication. However, RSEs for all these estimates are available free-of-charge on the ABS web site <www.abs.gov.au>, released in spreadsheet format as an attachment to this publication, Household Use of Information Technology, Australia, 2008–09 (cat. no. 8146.0).
CALCULATION OF STANDARD ERRORS
5 SEs can be calculated using the estimates (counts or means) and the corresponding RSEs. For example Table 4.3 shows that the estimated number of households with internet access in 2008–08 is 5,787,000. In the corresponding RSE table (See RSE table data cube for table 4.3), the RSE for this estimate is shown to be 1%. The SE is:
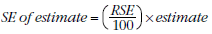
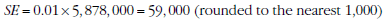
6 Therefore there are about two chances in three that the value that would have been produced if all dwellings had been included in the survey will fall within the range 5,819,000 to 5,937,000 and about 19 chances in 20 that the value will fall within the range 5,760,000 to 5,996,000.
PROPORTIONS AND PERCENTAGES
7 Proportions and percentages formed from the ratio of two estimates are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. A formula to approximate the RSE of a proportion is given below. This formula is only valid when x is a subset of y.
![Equation: RSE (x / y) = square root of ([RSE (x)] squared - [RSE (y)] squared)](/ausstats/abs@.nsf/0/101878733157bf53ca25796600153086/Body/0.2D14!OpenElement&FieldElemFormat=gif)
8 For example in Table 4.3 the estimate for the proportion of households in the Northern Territory with broadband access in terms of those with internet access is 87%.
9 From RSE Table 4.3 data cube corresponding to Table 4.3, the RSE of the estimated number of households in the Northern Territory with broadband access is 4%, and the RSE of the estimated number of households in the Northern Territory with internet access is 3%.
10 Applying the above formula, the RSE of the proportion is:
![Equation: RSE (x / y) = square root of ([4] squared - [3] squared) = 2.6% (rounded to one decimal place)](/ausstats/abs@.nsf/0/101878733157bf53ca25796600153086/Body/0.38BA!OpenElement&FieldElemFormat=gif)
11 This then gives an SE for the proportion (87%) of 0.026 x 87 = 2 percentage points.
12 Therefore there are about two chances in three that the proportion of households in the Northern Territory with broadband access is between 85% and 89%, and 19 chances in 20 that the proportion is within the ranges 83% to 91%.
DIFFERENCES
13 Published estimates may also be used to calculate the difference between two survey estimates (of numbers or percentages). Such an estimate is subject to sampling error. The sampling error of the difference between two estimates depends on their SEs and the relationship (correlation) between them. An approximate SE of the difference between two estimates (x-y) may be calculated by the following formula:
![Equation: SE (x - y) = square root of ([SE (x)] squared - [SE (y)] squared)](/ausstats/abs@.nsf/0/101878733157bf53ca25796600153086/Body/0.48FE!OpenElement&FieldElemFormat=gif)
14 From Table 4.3, it is estimated that 5,878,000 households had access to the internet in the home in 2008–09. This estimate has an RSE of 1% (see Table on page 106), which corresponds to a standard error of around 59,000 (see paragraph 5 above). The corresponding figure for 2007–08 was 5,492,000, with a standard error of around 55,000. The estimated increase in number of households with home internet access from the previous year is therefore 386,000. Using the above formula the SE of the change in household internet connections is around 81,000. Hence there are about two chances in three that the true value is within the range 305,000 to 467,000 households and about 19 chances in 20 that the true value is within the range 224,000 to 548,000 households.
15 While this formula will only be exact for differences between separate and uncorrelated characteristics or subpopulations, it is expected to provide a good approximation for all differences likely to be of interest in this publication.
SIGNIFICANCE TESTING
16 The statistical significance test for any of the comparisons between estimates was performed to determine whether it is likely that there is a difference between the corresponding population characteristics. The standard error of the difference between two corresponding estimates (x and y) can be calculated using the formula in paragraph 13. This standard error is then used to calculate the following test statistic:
![Equation: Test statistic = ([x - y] / [SE(x - y)])](/ausstats/abs@.nsf/0/101878733157bf53ca25796600153086/Body/0.57E2!OpenElement&FieldElemFormat=gif)
17 If the value of this test statistic is greater than 1.96 then we may say there is good evidence of a real difference in the two populations with respect to that characteristic. Otherwise, it cannot be stated with confidence that there is a real difference between the populations.
18 The imprecision due to sampling variability, which is measured by the SE, should not be confused with inaccuracies that may occur because of imperfections in reporting by respondents and recording by interviewers, and errors made in coding and processing data. Inaccuracies of this kind are referred to as non-sampling error, and they occur in any enumeration, whether it be a full count or sample. Every effort is made to reduce non-sampling error to a minimum by careful design of questionnaires, intensive training and supervision of interviewers, and efficient operating procedures.
 Print Page
Print Page
 Print All
Print All
 Quality Declaration
Quality Declaration