TECHNICAL NOTE DATA QUALITY
RELIABILITY OF THE ESTIMATES
1 Since the estimates in this publication are based on information obtained from occupants of a sample of dwellings, they are subject to sampling variability. That is, they may differ from those estimates that would have been produced if all occupants of all dwellings had been included in the survey. One measure of the likely difference is given by the standard error (SE), which indicates the extent to which an estimate might have varied by chance because only a sample of dwellings (or occupants) was included. There are about two chances in three (67%) that a sample estimate will differ by less than one SE from the number that would have been obtained if all dwellings had been included, and about 19 chances in 20 (95%) that the difference will be less than two SEs.
2 Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate:
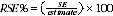
3 RSEs for estimates from Environmental Issues: Energy Use and Conservation 2008 are published for the first time in 'direct' form. Previously a statistical model was produced that related the size of estimates to their corresponding RSEs, and this information was displayed via a 'SE table'. From now on, RSEs for Environmental Issues: Energy Use and Conservation estimates will be calculated for each separate estimate and published individually. The Jackknife method of variance estimation is used for this process, which involves the calculation of 30 'replicate' estimates based on 30 different subsamples of the original sample. The variability of estimates obtained from these subsamples is used to estimate the sample variability surrounding the main estimate.
4 Limited publication space does not allow for the separate indication of the SEs and/or RSEs of all the estimates in this publication. However, RSEs for all these estimates will be available free-of-charge on the ABS website <www.abs.gov.au>.
5 In the tables in this publication, only estimates (numbers and proportions) with RSEs less than 25% are considered sufficiently reliable for most purposes. However, estimates with larger RSEs have been included and are preceded by an asterisk (e.g. *3.4) to indicate they are subject to high SEs and should be used with caution. Estimates with RSEs greater than 50% are preceded by a double asterisk (e.g. **2.1) to indicate that they are considered too unreliable for general use.
PROPORTIONS AND PERCENTAGES
6 Proportions formed from the ratio of two estimates are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. A formula to approximate the RSE of a proportion is given below. This formula is only valid when x is a subset of y.
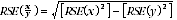
DIFFERENCES
7 Published estimates may also be used to calculate the difference between two survey estimates (of numbers or percentages). Such an estimate is subject to sampling error. The sampling error of the difference between two estimates depends on their SEs and the relationship (correlation) between them. An approximate SE of the difference between two estimates (x-y) may be calculated by the following formula:
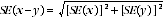
8 While this formula will only be exact for differences between separate and uncorrelated characteristics or subpopulations, it is expected to provide a good approximation for all differences likely to be of interest in this publication.
SIGNIFICANCE TESTING
9 The statistical significance test for any of the comparisons between estimates can be performed to determine whether it is likely that there is a difference between the corresponding population characteristics. The standard error of the difference between two corresponding estimates (x and y) can be calculated using the formula in paragraph 7. This standard error is then used to calculate the following test statistics:
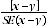
10 If the value of this test statistic is greater than 1.96 then we may say there is good evidence of a real difference (at the 95% confidence interval level) in the two populations with respect to that characteristic. Otherwise, it cannot be stated with this level of confidence that there is a real difference between the populations.
11 The imprecision due to sampling variability, which is measured by the SE, should not be confused with inaccuracies that may occur because of imperfections in reporting by respondents and recording by interviewers, and errors made in coding and processing data. Inaccuracies of this kind are referred to as non-sampling error, and they occur in any enumeration, whether it be a full count or sample. Every effort is made to reduce non-sampling error to a minimum by careful design of questionnaires, intensive training and supervision of interviewers, and efficient operating procedures.
 Print Page
Print Page
 Print All
Print All
 Quality Declaration
Quality Declaration