TECHNICAL NOTE DATA QUALITY
RELIABILITY OF THE ESTIMATES
1 Estimates in this publication are subject to sampling and non-sampling errors.
Non-Sampling Errors
2 Non-sampling errors are inaccuracies that occur because of imperfections in reporting by respondents and interviewers, and errors made in coding and processing data. These inaccuracies may occur in any enumeration, whether it be a full count or a sample. Every effort is made to reduce the non-sampling error to a minimum by careful design of questionnaires, intensive training and supervision of interviewers, and effective processing procedures.
Sampling Errors
3 As the estimates in this publication are based on information obtained from a sample of households and persons, they are subject to sampling variability. That is, they may differ from the figures that would have been produced if all households and persons in Australia had been included in the survey. One measure of the likely difference is given by the standard error (SE), which indicates the extent to which an estimate might have varied by chance because only a sample of households and persons was included. There are about 2 chances in 3 (67%) that a sample estimate will differ by less than one SE from the figure that would have been obtained if all households and persons had been included in the survey, and about 19 chances in 20 (95%) that the difference will be less than two SEs.
4 Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate. The RSE is determined by dividing the SE of an estimate SE(x) by the estimate x and expressing it as a percentage. That is (where x is the estimate):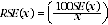 
5 In general, the size of the SE increases as the size of the estimate increases. Conversely, the RSE decreases as the size of the estimate increases. Very small estimates are thus subject to such high RSEs that their value for most practical purposes is unreliable.
6 In the tables in this publication, only estimates with RSEs of 25% or less are considered reliable for most purposes. Estimates with RSEs greater than 25% but less than or equal to 50% are preceded by an asterisk (e.g. *3.4) to indicate they are subject to high SEs and should be used with caution. Estimates with RSEs of greater than 50%, preceded by a double asterisk (e.g. **0.3), are considered too unreliable for general use and should only be used to aggregate with other estimates to provide derived estimates with RSEs of less than 25%.
7 Space does not allow for the separate indication of SEs and/or RSEs of all the estimates in this publication. However, RSEs for all of these estimates are available free-of-charge on the ABS web site <www.abs.gov.au>, to be released in July in spreadsheet format as an attachment to this publication, Personal Fraud, Australia, 2007 (cat. no. 4528.0).
USING STANDARD ERRORS FOR POPULATION ESTIMATES
8 An example of the calculation and use of SEs for estimates of persons follows. Table 1 shows that the estimated number of victims of credit card fraud is 383,300. In the RSE spreadsheet table, the RSE for this estimate is shown to be 6.4%. The SE is: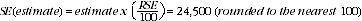 
9 Thus there are about two chances in three that the value that would have been obtained, had all persons been included in the survey, lies between 358,800 and 407,800. Similarly, there are about 19 chances in 20 that the true value lies between 334,300 and 432,300.
10 Proportions and percentages formed from the ratio of two estimates are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. A formula for the RSE of a proportion or a percentage is as shown: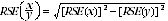 
. This formula is only valid when x is a subset of y.
WEIGHTING, BENCHMARKS AND ESTIMATION
11 Weighting is the process of adjusting results from a sample survey to infer results for the total in-scope population. To do this, a 'weight' is allocated to each sample unit. For the Personal Fraud Survey, each sample unit is a person. The weight is a value that indicates how many population units are represented by the sample unit.
12 The first step in calculating weights for each unit is to assign an initial weight, which is the inverse of the probability of being selected in the survey. For example, if one person in every three were selected to participate in a survey (that is, one-third of the total in scope population), the weight given to each sample unit would be 3.
Benchmarking
13 The initial weights are then calibrated to align with independent estimates of the population of interest, referred to as 'benchmarks'. This is done to ensure that the survey estimates conform to the independently estimated distribution of the population rather than the distribution within the sample itself.
14 The Personal Fraud Survey was benchmarked to the estimated civilian population aged 15 years and over living in private dwellings in each state and territory excluding persons out of scope (see Explanatory Notes 6 to 8). The process of weighting ensures that the survey estimates conform to person benchmarks by state, part of state, age and sex. These benchmarks are produced from estimates of the resident population derived independently of the survey.
Estimation
15 Survey estimates of counts of persons are then obtained by summing the weights of persons with the characteristic of interest.
Quality Declaration 
Print Page
Print All