This document was added or updated on 13/12/2013.
METHODOLOGY
SELECTION OF SAMPLE
Data in the Census Sample Files (CSFs) represent 1% and 5% samples of all dwelling, family and person records from the 2011 Census of Population and Housing.
The 1% Basic CSF provides a sample of one private dwelling record in every hundred from the Census, and the associated family and person records. Dwellings with more than six usual residents were removed from the sample to ensure confidentiality of large dwellings (see Large households). For non-private dwellings the sampling is applied to persons present, where one person in every hundred is selected and the associated dwelling records included on the file.
The 5% Expanded CSF provides a sample of one private dwelling in every twenty from the Census, and the associated family and person records. Dwellings with more than eight usual residents were removed from the sample to ensure confidentiality of large dwellings (see Large households). For non-private dwellings the sampling is applied to persons present, where five persons in every hundred are selected and the associated dwelling records included on the file.
The 1% CSF and the 5% CSF also contain corresponding family and person records for the selected private dwellings, as well as a 1 in 100 (or 1 in 20) sample of person records from non-private dwellings. Person, family and dwelling estimates can be obtained from the CSF for private dwellings, but only person level estimates are available for non-private dwellings, and hence for the whole Census population.
Large households
To ensure the confidentiality of large households in occupied private dwellings, the number of persons for each household is restricted to a maximum of six usual residents on the 1% Basic CSF and eight usual residents on the 5% Expanded CSF. Dwellings with more than six usual residents for the 1% Basic CSF, or eight usual residents for the 5% Expanded CSF, have been replaced by dwellings of a similar size and from a similar region that do not have more than the maximum number of usual residents.
Persons in Other Territories, comprising Jervis Bay, Cocos (Keeling) and Christmas Islands, have been excluded from the sample, as have migratory, shipping and off-shore statistical areas.
Changes in previous CURFs can be found in Changes from previous CSF.
ESTIMATION PROCEDURE
An estimate of the total for an item can be obtained by totalling the item for the CSF and then multiplying the result by 100 for the 1% CSF, or by 20 for the 5% CSF. Note that this estimate of total will not correspond exactly to the total that would be obtained from the full Census, firstly because of the exclusion of large dwellings from the CSF, and secondly because of the sampling error arising due to the CSF containing only a sample of Census records.
Averages from the CSF, such as the proportion of persons falling into a particular category, can be used as an estimate of the corresponding average in the Census. For example, the proportion of Australian-born persons who are students is estimated by the proportion of students observed among Australian-born persons on the CSF. Note that if the denominator of such a proportion is known from the full Census then it can be multiplied by the estimated proportion to give an estimate of the numerator. For example, the total number of Australian-born students could be estimated by multiplying the above proportion by the Australian-born population. This gives an alternative estimate from the CSF (rather than counting the Australian-born students on the 1% CSF and multiplying by 100) that may be preferred in some circumstances, since it is more compatible with the known full-Census count.
RELIABILITY OF ESTIMATES
The sampling error should be taken into account when interpreting estimates from the CSF. A measure of the likely difference between an estimate from the CSF and the corresponding full Census value is given by the standard error (SE) of the estimate. The SE indicates the extent to which an estimate might have varied by chance because only a sample of persons was included. There are about two chances in three that a sample estimate will differ by less than one SE from the full Census value, and about 19 chances in 20 that the difference will be less than two SEs. Another measure of sampling variability is the relative standard error (RSE) which is obtained by expressing the SE as a percentage of the estimate to which it refers.
Non-sampling errors may occur in any enumeration - a full count or a sample - and should not be confused with imprecision due to sampling error, which is measured by the SE. Non-sampling errors in the CSF are differences due to the exclusion of large dwellings, while in the Census as a whole there may be inaccuracies that occur because of imperfections in reporting by respondents, errors made in collection (such as when recording responses) and errors made in processing the Census data. It is not possible to quantify non-sampling error, but every effort is made to reduce it to a minimum. For the following examples, non-sampling error is assumed to be zero. In practice, the potential for non-sampling error adds to the uncertainty in the estimates that is caused by sampling variability.
Standard error calculation
Both CSFs can be treated, for the purposes of standard error calculations, as a simple random sample of dwellings from the private dwelling population. For many purposes the non-private dwelling population has only a minor influence on results, and it is sufficient to include each person counted in a non-private dwelling as a separate 'dwelling' when calculating standard errors.
Dwelling level estimates
Estimates of the SE of averages for dwelling-level items can be obtained using standard formulae for a simple random sample. These standard error formulae require computing the average value of an item of interest per dwelling on the CSF. The formula for 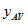 , the estimated average of an item that takes value
, the estimated average of an item that takes value  for dwelling d out of n sampled dwellings in a geographic area, is:
for dwelling d out of n sampled dwellings in a geographic area, is:
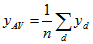
where 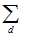 represents summing over the n dwellings.
represents summing over the n dwellings.
The standard error estimate 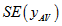 is given by the following formula:
is given by the following formula:
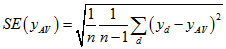
The estimate 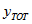 of the total count for this item, and its corresponding SE estimate
of the total count for this item, and its corresponding SE estimate  , are obtained by multiplying the average per dwelling by the number of dwellings in the geographic area. The number of dwellings is approximated with minimal error by:
, are obtained by multiplying the average per dwelling by the number of dwellings in the geographic area. The number of dwellings is approximated with minimal error by:
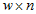
where w is the weight (100 on the 1% CSF, and 20 on the 5% CSF)
since the construction of the CSF ensures proportional representation of geographic areas. The formulae are as follows:
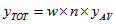
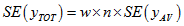
Note that the geographic area to be used in these calculations should be the smallest geographic area containing the dwellings in question. For example, estimates for a single state should use state as the geographic area.
Person level estimates
The above formulae can be applied to totals of persons by treating the
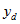
as person counts within the dwelling i.e.
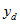
is the number of persons from dwelling d with the characteristic of interest. This makes
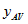
the average number of persons per dwelling having this characteristic, and
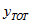
the total number of persons in the geographic area with this characteristic.
Family level estimates
Similarly, estimates for family-level items can be obtained by treating the
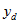
as family counts within the dwelling i.e.
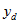
is the number of families from dwelling d with the characteristic of interest,
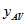
is the average number of families per dwelling having the characteristic, and
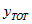
is the total number of families in the geographic area with the characteristic.
Example of standard error calculation
The Australian-born population of Australia from the 2011 Census is 15,017,845. As the CSF is based on place of enumeration counts, this figure can be obtained from the
Place of Enumeration Profile for Australia on the ABS website. However, as the CSF excludes Other Territories, 1,728 Australian-born persons enumerated in Other Territories on Census Night should be excluded, giving a total of 15,016,117 Australian-born persons. Note that persons enumerated in shipping, migratory or off-shore statistical areas
are also excluded from the CSF, but as these counts should be minor, and are not easily accessible from the ABS website, they have been ignored from the calculations.
The 1% CSF estimate of this figure is calculated by taking the 149,324 Australian-born persons on the 1% CSF and multiplying it by 100, giving an estimate of
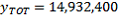 .
. The difference between this figure and the full Census figure of 15,016,117 is due to both the exclusion of large dwellings from the CSF and also the sampling error of the CSF estimate. Note that similar calculations can be carried out using data from the 5% CSF, but using a weight of 20. For simplicity, the remaining examples will be based on the 1% CSF figures.
The simplest way to calculate the SE of this estimate is to produce a file with a single record for each dwelling (treating each person from non-private dwellings as a separate dwelling). On this file, the item
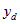
should give the number of Australian-born persons in the dwelling. A simple aggregation can be applied to this file to calculate
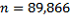
(the count of dwelling records),
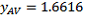
(the mean) and
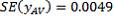
(the standard error of the mean). These are then used to estimate the total and its SE:
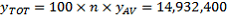
(as calculated previously), and
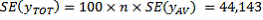
This SE calculation suggests that there are about two chances in three that the sample estimate will differ by less than 44,143
. from the full-Census value, and about 19 chances in 20 that the difference will be less than 2
x44,143
= 88,286 . The range (14,932,400 - 88,286; 14,932,400 + 88,286) = ( 14,844,114; 15,020,686) is known as the 95% confidence interval. In this example the Census value of 15,016,117 lies within the confidence interval range.
The estimate is low because the CSF excludes some 1,523 persons from large dwellings, approximately 69% of whom would have been born in Australia. This corresponds to excluding approximately 1,523 x 100 x 69% = 105,087 persons from the estimate. Ignoring the effect that these extra people would have had on the standard error, they would increase the estimate to approximately 15,037,487 Australian-born persons and the 95% confidence interval to (15,037,487 - 88,286; 15,037,487+ 88,286) = ( 14,949,201; 15,125,773). Whilst the initial confidence interval just covers the true value, the revised confidence interval more comfortably covers the true population value of 15,016,117.
Users may wish to reproduce these figures using the CSF to ensure that they have interpreted the calculations required correctly.
Clustering of the person sample
For some person-level variables, it may be a reasonable approximation to treat the CSF as a simple random sample of
persons, even though it is in fact a sample of dwellings. This would involve letting d in the above formulae indicate persons rather than dwellings, and replacing n by the number of persons in the CSF geographic area of interest. Person means and associated standard errors could then be obtained by a standard tabulation package applied to the person-level data.
Unfortunately, doing this will typically give an underestimate of the actual SE. The extent of this underestimation depends on how clustered the variable of interest is within dwellings - that is, on how often similar values of the variable tend to occur together in the same dwelling. The understatement of standard error will be greatest for variables that are highly clustered within dwellings, such as birthplace.
For this reason it would be appropriate, when treating the CSF as a sample of persons, to obtain a measure of the effect of clustering for the variables being investigated. A suitable measure is the design factor (DEFT), given by the ratio of the SE calculated correctly (with dwellings as units) to the SE calculated treating persons as units. Standard errors from the person-level analysis can then be adjusted by this factor.
The SE ignoring clustering will be denoted by
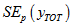
, with the subscript p indicating that it is calculated at the person level. This can be obtained by taking the person-level CSF and creating a variable taking the value 1 for Australian-born persons and 0 otherwise. Applying a simple tabulation package to this person-level file gives
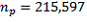
(the count of person records),
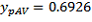
(the mean) and
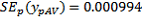
(the standard error of the mean). These are then used to estimate the total and its SE.
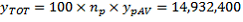
(as calculated previously) and
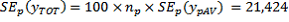
The design factor is then given as

Thus the standard error produced ignoring clustering underestimates the actual standard error by a factor of 2. Users could expect that other totals (eg. for geographic regions) for the variable 'Australian-born' would have a similar design factor.
Standard errors for proportions and differences
Proportions
Simple approximations can be used to estimate the standard error for a ratio of counts. If 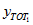 and
and  are estimated totals for two nested categories (i.e. category 2 is a subset of category 1) then writing
are estimated totals for two nested categories (i.e. category 2 is a subset of category 1) then writing 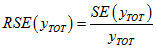
for the relative standard error gives the following approximation:
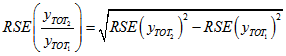
This formula depends on the two categories being nested, and should not be used for distinct categories.
Differences
If two totals are for distinct categories (eg. in comparing estimates across states) then the difference between two totals has the following SE approximation:
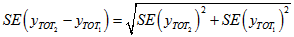
While this formula will only be exact for differences between separate and uncorrelated (unrelated) characteristics or sub-populations, it is expected to provide a good approximation for most differences likely to be of interest.
Example of a standard error calculation for a proportion
The number of Australian-born persons who are full-time students (STUP=2) can be estimated by producing a dwelling-level file with a variable  giving the number of Australian-born full-time students in the dwelling. Tabulating this variable gives
giving the number of Australian-born full-time students in the dwelling. Tabulating this variable gives  ,
, 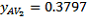 ,
, 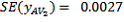 , so that:
, so that:
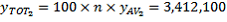 ,
,
and
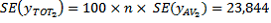
Thus there are an estimated 3,412,100 Australian-born full-time students, with a SE of 23,844 and an
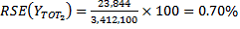 .
.
The RSE of the estimate of Australian-born persons is
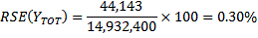
(see earlier calculations).
Thus the estimated proportion of Australian-born persons who are full-time students is given by
 =
= 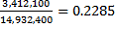 .
.
The RSE of this proportion is estimated as

Thus, the RSE on the estimated proportion of 0.2285 is 0.63% and hence the SE is 0.0014.
Regression estimates
One use of the sample file will be to examine relationships between variables using regression methods. By treating the dwelling as the sample unit, standard regression packages can be used unweighted and the resulting standard errors and test statistics will be good estimates. For example, a regression model could be derived for 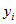 , the number of persons in the dwelling needing assistance with core activities, against various characteristics
, the number of persons in the dwelling needing assistance with core activities, against various characteristics 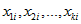 Equation such as
Equation such as 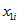 , the number of persons in the dwelling aged over 65 years, to fit the linear regression model:
, the number of persons in the dwelling aged over 65 years, to fit the linear regression model:
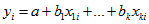
Measures of model fit and of significance of the parameters 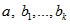 from the standard package will then be appropriate. Unfortunately such a linear model may not adequately describe the relationships between variables at a dwelling level.
from the standard package will then be appropriate. Unfortunately such a linear model may not adequately describe the relationships between variables at a dwelling level.
If a similar regression is performed treating person as the sample unit, the resulting standard errors and measures of significance could be inaccurate or misleading. This arises because the persons in the sample are clustered within dwellings, and so their responses may be "correlated" or affected by similar influences such as characteristics of the dwelling. The extent to which the measures of significance are affected will depend on how clustered the variable 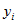 is likely to be within dwellings.
is likely to be within dwellings.
If a person-level analysis is performed, such as a 'logistic analysis' of the probability of a person having a given characteristic, then the effect of clustering should be taken into account when interpreting the outcomes. In particular, SEs are likely to be understated, as discussed in the section Clustering of the person sample, and this will tend to increase the apparent significance of modelled effects.
Techniques are available to perform valid analyses at the person level for a sample that is clustered within dwellings, treating persons as being subject to both person and dwelling effects. These techniques include 'multi-level', 'random effect' and 'mixed' modelling. (Footnote 1 and 2)
By using these techniques, models can be used that do a better job of describing the actual relationships between variables at both person and dwelling level. Statistical packages are widely available to validly perform such analyses.
___________________________
Footnote 1 Goldstein, H. and Arnold, E, 1995, 'Multilevel Statistical Models', 2nd ed.Halsted Press, New York.
Footnote 2 Snijders Tom A. B. and Bosker Roel J, 1999, 'Multilevel analysis : an introduction to basic and advanced multilevel modelling, SAGE, London.
 Print Page
Print Page
 Print All
Print All