TECHNICAL NOTE DATA QUALITY
RELIABILITY OF THE ESTIMATES
NON-SAMPLING ERRORS
1 Errors other than those due to sampling may occur in any type of collection and are referred to as non-sampling error. For this survey, non-sampling error can be introduced through inadequacies in the questionnaire, non-response, inaccurate reporting by respondents, errors in the application of survey procedures, incorrect recording of answers and errors in data entry and processing. The extent to which non-sampling error affects the results of the survey is not precisely quantifiable. Every effort was made to minimise non-sampling error by careful design and testing of the questionnaire, efficient operating procedures and systems and the use of appropriate methodology.
SAMPLING ERRORS
2 Since the estimates in this publication are based on information obtained from occupants of a sample of dwellings, they are subject to sampling variability. That is, they may differ from the population parameter that would have been obtained if all occupants of all dwellings had been enumerated in the survey. One measure of the likely difference is given by the standard error (SE), which indicates the extent to which an estimate might have varied by chance from the population parameter because only a sample of dwellings (or occupants) was enumerated. There are about two chances in three (67%) that a sample estimate will differ by less than one SE from the number that would have been obtained if all dwellings had been enumerated, and about 19 chances in 20 (95%) that the difference will be less than two SEs.
3 Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate:
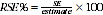
4 RSEs for estimates from 2010 Flexible Working Arrangements in Queensland survey are published for each individual data cell. The Jackknife method of variance estimation has been used to produce RSE estimates for this publication. This variance estimation method involves the calculation of 30 'replicate' estimates based on sub-samples of the original sample. The variability of estimates obtained from these sub-samples is used to estimate the sample variability for the main estimate.
5 In the data cubes in this publication RSEs are published for each individual data cell. Only estimates (numbers and proportions) with RSEs less than 25% are considered sufficiently reliable for most purposes. However, estimates with larger RSEs have been included and annotated to indicate they are subject to high uncertainty and should be used with caution.
ESTIMATION PROCEDURE
6 The estimates in this publication were obtained using a post-stratification procedure. This procedure ensured that the survey estimates conformed to an independently estimated distribution of the population, by state, part of state, age and sex, rather than the observed distribution among respondents.
PROPORTIONS AND PERCENTAGES
7 Proportions formed from the ratio of two estimates are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. A formula to approximate the RSE of a proportion is given below. This formula is only valid when x is a subset of y.
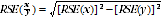
DIFFERENCES
8 Published estimates may also be used to calculate the difference between two survey estimates (of numbers or percentages). Such an estimate is subject to sampling error. The sampling error of the difference between two estimates depends on their SEs and the statistical association (correlation) between the estimates. An approximate SE of the difference between two estimates (x-y) may be calculated by the following formula:

9 While this formula will only be exact for differences between separate and uncorrelated characteristics or subpopulations, it is expected to provide a good approximation for all differences likely to be of interest in this publication.
SIGNIFICANCE TESTING
10 A statistical significance test can be performed to indicate whether the survey provides sufficient evidence that a difference between two survey estimates reflects an actual difference in the population. The following measure, called a "test statistic", can be used to test the statistical significance of a difference between two survey estimates. (The standard error of the difference between two corresponding estimates (x and y) can be calculated using the formula in paragraph 10.)
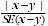
11 If the value of this test statistic is greater than 1.96, then we may say there is strong evidence the difference between the survey estimates reflects a difference in the population.
 Print Page
Print Page
 Print All
Print All
 Quality Declaration
Quality Declaration