TECHNICAL NOTE
RELIABILITY OF ESTIMATES
1 Two types of error are possible in an estimate based on a sample survey: sampling error and non-sampling error. The sampling error is a measure of the variability that occurs by chance because a sample, rather than the entire population, is surveyed. Since the estimates in this publication are based on information obtained from occupants of a sample of dwellings they are subject to sampling variability; that is, they may differ from the figures that would have been produced if all dwellings had been included in the survey. One measure of the likely difference is given by the standard error (SE). There are about two chances in three that a sample estimate will differ by less than one SE from the figure that would have been obtained if all dwellings had been included, and about 19 chances in 20 that the difference will be less than two SEs.
2 Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate. The RSE is a useful measure in that it provides an immediate indication of the percentage errors likely to have occurred due to sampling, and thus avoids the need to refer also to the size of the estimate.

3 RSEs for published estimates are supplied in Excel data tables, available via the Downloads page.
4 The smaller the estimate the higher is the RSE. Very small estimates are subject to such high SEs (relative to the size of the estimate) as to detract seriously from their value for most reasonable uses. In the tables in this publication, only estimates with RSEs less than 25% are considered sufficiently reliable for most purposes. However, estimates with larger RSEs, between 25% and less than 50% have been included and are preceded by an asterisk (eg *3.4) to indicate they are subject to high SEs and should be used with caution. Estimates with RSEs of 50% or more are preceded with a double asterisk (eg**0.6). Such estimates are considered unreliable for most purposes.
5 The imprecision due to sampling variability, which is measured by the SE, should not be confused with inaccuracies that may occur because of imperfections in reporting by interviewers and respondents and errors made in coding and processing of data. Inaccuracies of this kind are referred to as the non-sampling error, and they may occur in any enumeration, whether it be in a full count or only a sample. In practice, the potential for non-sampling error adds to the uncertainty of the estimates caused by sampling variability. However, it is not possible to quantify the non-sampling error.
STANDARD ERRORS OF PROPORTIONS AND PERCENTAGES
6 Proportions and percentages formed from the ratio of two estimates are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. For proportions where the denominator is an estimate of the number of persons in a group and the numerator is the number of persons in a sub-group of the denominator group, the formula to approximate the RSE is given below. The formula is only valid when x is a subset of y.
![Equation: RSE (x / y) = square root of ([RSE (x)] squared - [RSE (y)] squared)](/ausstats/abs@.nsf/0/9952ce82e847e6a3ca2580ed0012b0fc/Body/0.2104!OpenElement&FieldElemFormat=gif)
COMPARISON OF ESTIMATES
7 Published estimates may also be used to calculate the difference between two survey estimates. Such an estimate is subject to sampling error. The sampling error of the difference between two estimates depends on their SEs and the relationship (correlation) between them. An approximate SE of the difference between two estimates (x-y) may be calculated by the following formula:
![Equation: SE (x minus y) = square root of ([RSE (x)] squared + [RSE (y)] squared)](/ausstats/abs@.nsf/0/9952ce82e847e6a3ca2580ed0012b0fc/Body/0.3642!OpenElement&FieldElemFormat=gif)
8 While the above formula will be exact only for differences between separate and uncorrelated (unrelated) characteristics of sub-populations, it is expected that it will provide a reasonable approximation for all differences likely to be of interest in this publication.
9 Another measure is the Margin of Error (MOE), which describes the distance from the population value that the sample estimate is likely to be within, and is specified at a given level of confidence. Confidence levels typically used are 90%, 95% and 99%. For example, at the 95% confidence level the MOE indicates that there are about 19 chances in 20 that the estimate will differ by less than the specified MOE from the population value (the figure obtained if all dwellings had been enumerated). The 95% MOE is calculated as 1.96 multiplied by the SE.
10 The 95% MOE can also be calculated from the RSE by:

11 The MOEs in this publication are calculated at the 95% confidence level. This can easily be converted to a 90% confidence level by multiplying the MOE by:
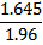
or to a 99% confidence level by multiplying by a factor of:
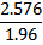
12 A confidence interval expresses the sampling error as a range in which the population value is expected to lie at a given level of confidence. The confidence interval can easily be constructed from the MOE of the same level of confidence by taking the estimate plus or minus the MOE of the estimate.
SIGNIFICANCE TESTING
13 For comparing estimates between surveys or between populations within a survey it is useful to determine whether apparent differences are 'real' differences between the corresponding population characteristics or simply the product of differences between the survey samples. One way to examine this is to determine whether the difference between the estimates is statistically significant. This is done by calculating the standard error of the difference between two estimates (x and y) and using that to calculate the test statistic using the formula below:
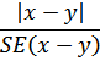
where
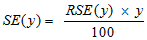
14 If the value of the statistic is greater than 1.96 then we may say there is good evidence of a statistically significant difference at 95% confidence levels between the two populations with respect to that characteristic. Otherwise, it cannot be stated with confidence that there is a real difference between the populations.
 Print Page
Print Page
 Print All
Print All