• Summary
• Downloads
• Explanatory Notes
• Related Information
• Past Releases

TECHNICAL NOTE DATA QUALITY


INTRODUCTION

1 Since the estimates in this publication are based on information obtained from occupants of a sample of dwellings, they are subject to sampling variability. That is, they may differ from those estimates that would have been produced if all dwellings had been included in the survey. One measure of the likely difference is given by the standard error (SE), which indicates the extent to which an estimate might have varied by chance because only a sample of dwellings was included. There are about two chances in three (67%) that a sample estimate will differ by less than one SE from the number that would have been obtained if all dwellings had been included, and about 19 chances in 20 (95%) that the difference will be less than two SEs. Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate.

2 Due to space limitations, it is impractical to print the SE of each estimate in the publication. Instead, a table of SEs is provided to enable readers to determine the SE for an estimate from the size of that estimate (see table T1). The SE table is derived from a mathematical model, referred to as the 'SE model', which is created using the data collected in this survey. It should be noted that the SE model only gives an approximate value for the SE for any particular estimate, since there is some minor variation between SEs for different estimates of the same size.

CALCULATION OF STANDARD ERROR

3 An example of the calculation and the use of SEs in relation to estimates of persons is as follows. Table 1 shows that in 2005-06, the estimated number of women in Australia who worked at some time in the last 12 months was 4,944,300. Since this estimate is between 2,000,000 and 5,000,000, table T1 shows that the SE for Australia will lie between 25,000 and 32,700 and can be approximated by interpolation using the following general formula:

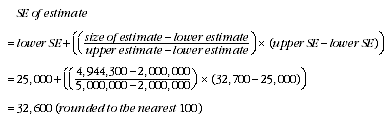
4 Therefore, there are about two chances in three that the value that would have been produced if all dwellings had been included in the survey will fall within the range 4,911,700 to 4,976,900 and about 19 chances in 20 that the value will fall within the range 4,897,100 to 5,009,500. This example is illustrated in the diagram below.

PROPORTIONS AND PERCENTAGES

6 Proportions and percentages formed from the ratio of two estimates are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. A formula to approximate the RSE of a proportion is given below. This formula is only valid when x is a subset of y.

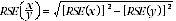
7 Considering the example from the previous page, of the 4,944,300 women who worked at some time in the last 12 months, 251,900 or 5.1% experienced a work-related injury or illness. The SE of 251,900 may be calculated by interpolation as 12,000. To convert this to an RSE we express the SE as a percentage of the estimate, or 12,000/251,900 = 4.8%. The SE for 4,944,300 was calculated previously as 32,600, which converted to an RSE is 32,600/4,944,300 = 0.7%. Applying the above formula, the RSE of the proportion is

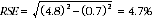
8 Therefore, the SE for the proportion of women who worked at some time in the last 12 months and who experienced a work-related injury or illness is 0.2 percentage points (=(5.1/100)x4.7). Therefore, there are about two chances in three that the proportion of women who worked at some time in the last 12 months and who experienced a work-related injury or illness is between 4.9% and 5.3% and 19 chances in 20 that the proportion is within the range 4.7% to 5.5%.

DIFFERENCES

9 Published estimates may also be used to calculate the difference between two survey estimates (of numbers or percentages). Such an estimate is subject to sampling error. The sampling error of the difference between two estimates depends on their SEs and the relationship (correlation) between them. An approximate SE of the difference between two estimates (x-y) may be calculated by the following formula:

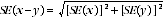
10 While this formula will only be exact for differences between separate and uncorrelated characteristics or subpopulations, it is expected to provide a good approximation for all differences likely to be of interest in this publication.

STANDARD ERRORS

T1 STANDARD ERRORS OF ESTIMATES
									AUST.
	NSW	Vic.	Qld	SA	WA	Tas.	NT	ACT	SE	RSE
Size of estimate (persons)	no.	no.	no.	no.	no.	no.	no.	no.	no.	%
100	250	280	260	180	250	120	120	110	170	170.0
200	390	420	390	260	360	190	200	180	270	135.0
300	500	520	490	330	440	250	260	250	350	116.7
500	670	690	650	430	570	330	360	350	490	98.0
700	820	820	790	510	680	400	440	430	610	87.1
1,000	1 000	990	950	610	800	490	540	530	760	76.0
1,500	1 250	1 210	1 170	750	970	610	660	670	970	64.7
2,000	1 460	1 390	1 350	850	1 110	700	760	780	1 150	57.5
2,500	1 650	1 550	1 500	950	1 200	800	850	850	1 300	52.0
3,000	1 800	1 700	1 650	1 050	1 300	850	900	950	1 450	48.3
3,500	1 950	1 800	1 750	1 100	1 400	900	950	1 000	1 600	45.7
4,000	2 100	1 950	1 900	1 150	1 500	1 000	1 000	1 100	1 700	42.5
5,000	2 350	2 150	2 100	1 300	1 650	1 100	1 100	1 200	1 900	38.0
7,000	2 750	2 500	2 450	1 500	1 900	1 250	1 250	1 350	2 300	32.9
10,000	3 250	2 900	2 850	1 750	2 200	1 450	1 400	1 550	2 800	28.0
15,000	3 900	3 450	3 350	2 050	2 600	1 750	1 550	1 750	3 400	22.7
20,000	4 450	3 900	3 800	2 300	2 900	1 950	1 650	1 900	3 950	19.8
30,000	5 300	4 600	4 450	2 700	3 350	2 250	1 750	2 050	4 800	16.0
40,000	6 000	5 150	4 950	3 000	3 700	2 450	1 850	2 200	5 500	13.8
50,000	6 550	5 600	5 350	3 250	4 050	2 650	1 900	2 300	6 100	12.2
100,000	8 600	7 300	6 850	4 150	5 100	3 300	2 000	2 500	8 250	8.3
150,000	10 000	8 400	7 800	4 750	5 800	3 700	2 000	2 550	9 800	6.5
200,000	11 050	9 250	8 550	5 200	6 350	3 950	2 000	2 600	11 000	5.5
300,000	12 700	10 600	9 650	5 850	7 200	4 350	15 400	2 550	12 950	4.3
500,000	14 950	12 500	11 150	6 800	8 300	4 850	. .	2 550	15 650	3.1
1,000,000	18 400	15 350	13 300	8 200	10 000	6 250	. .	. .	20 000	2.0
2,000,000	22 200	18 600	15 550	9 700	11 850	. .	. .	. .	25 000	1.3
5,000,000	27 650	23 400	18 600	13 000	11 500	. .	. .	. .	32 700	0.7
10,000,000	. .	36 450	15 250	. .	. .	. .	. .	. .	39 200	0.4
20,000,000	. .	. .	. .	. .	. .	. .	. .	. .	46 050	0.2
. . not applicable

T2 LEVELS AT WHICH ESTIMATES HAVE RELATIVE STANDARD ERRORS OF 25% AND 50%(a)
	NSW	Vic.	Qld.	SA	WA	Tas.	NT	ACT	Aust.
	no.	no.	no.	no.	no.	no.	no.	no.	no.
Estimate with 25% RSE	16 300	13 100	12 500	5 300	8 000	3 900	4 100	4 500	12 400
Estimate with 50% RSE	4 400	3 800	3 600	1 500	2 400	1 000	1 200	1 200	2 800
(a) Refers to the number of persons contributing to the estimate.